Vectorii în planul formulei și exemple

Vector în avion este direcționat segment de linie, în care unul dintre capetele intervalului (perioada) este începutul vectorului, iar al doilea - capătul său (figura 1.).

Dacă începutul și sfârșitul vectorului - un punct și apoi vectorul este desemnat. De asemenea, litere mici sunt folosite pentru a desemna vectori:

zero, vector

vector Nul este un vector a cărui origine coincide cu capătul (Fig. 1).

Zero vector dă orice direcție pe un plan.

Lungimea sau modulemvektora numit un întreg nenegativ egală cu lungimea segmentului care definește un vector.

Lungimea vectorului de zero este zero.

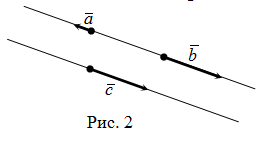
vectori coliniari și non-colineare ale planului

Doi vectori în planul numit coliniare. sau în cazul în care acestea se află pe aceeași linie sau pe liniile paralele (Fig. 2). În caz contrar, vectori se numesc coliniare.

Vectorul zero, este coliniar cu orice alt plan vector.

Co-direcționată și vectori direcționate opus pe planul

Doi vectori coliniare sunt numite codirectional. în cazul în care direcțiile lor sunt aceleași. vectori coliniari sunt identificate după cum urmează :. Doi vectori colineare se numesc direcția opusă. în cazul în care acestea sunt în direcții opuse. Desemnarea.

Se crede că vectorul de zero este codirectional cu orice alt plan vector.

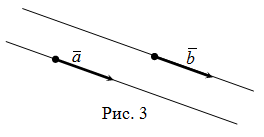
Doi vectori se numesc plane egale. în cazul în care au aceeași direcție și lungimile lor sunt egale (figura 3):

Vectorul se numește opusă vectorului, în cazul în care acești vectori sunt îndreptate în sens opus și lungimile lor sunt egale.

Amână dintr-un punct pe un plan și doi vectori de arbitrare (Fig. 4). Raze care emană din acest punct formează un unghi, numit unghiul dintre vectorii și:

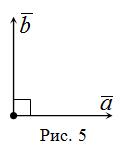
Unghiul Codirectional dintre vectori este egal (sau zero radiani) ca unghiul dintre vectorii - direcționate opus (sau radiani).

Doi vectori se numesc ortogonale (sau perpendicular) dacă unghiul dintre ele este (radian) (Fig. 5).