Înscrisă, cerc circumscris de triunghi

incircle

În cazul în care toate laturile triunghiului atinge cercul, apoi cercul se numește triunghiul și triunghi înscris - a descris despre cercul.

Teorema. În orice cerc triunghi poate fi înscris, și cu un singur.

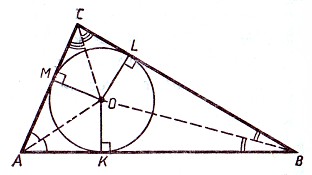
Centrul cercului înscris în triunghiul se află la intersecția Bisectors sale.

Dacă toate nodurile de minciuna poligon pe cerc, apoi cercul se spune că a fost descris despre triunghiul, și triunghiul - înscris în acest cerc.

Teorema. Despre orice triunghi poate fi descris într-un cerc și, în același timp, doar unul.

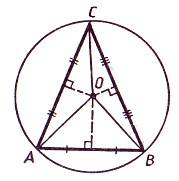
Centrul cercului circumscris triunghiului este la punctul de intersecție midperpendiculars.

Raza de aproximativ un triunghi echilateral, un cerc definit prin formula:

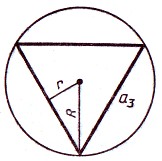
Raza cercului înscris într-un triunghi echilateral este definit de formula:

Centrul de cerc descris despre un triunghi dreptunghic, se află în mijlocul ipotenuzei sale.

Raza cercului în jurul triunghiului drept egal cu lungimea medianei trase la ipotenuzei.

Raza cercului inscris la un triunghi dreptunghic definit prin formula: