Cum de a găsi direcția de piață, știind zona sa

Formula standard pentru calcularea suprafeței unui dreptunghi este produsul dintre diferitele laturi și are forma: S = a * b, în ​​cazul în care s - zona unui avion figura, a și b din laturile sale având lungimi diferite. Pentru a calcula ploschadkvadrata. În formulele de mai sus trebuie să-l înlocuiască. Dar ei sunt, se pare, pentru a găsi zona de dreapta a dreptunghiului pe care trebuie să-l pătrat. S = (a), în al doilea grad.

Acum, în conformitate cu o formulă de zonă pătrat puteți să-l găsiți. știind valoarea numerică a zonei. Pentru aceasta este necesar să se rezolve ecuația de gradul doi: S = (a), în al doilea grad. Situat lateral „a“ este îndepărtat de valori de rădăcină pătrată figura: a = rădăcină pătrată din (S). Exemplu: pentru a găsi storonukvadrata. în cazul în care o suprafață de șaizeci și patru de centimetri pătrați. Soluție: Dacă 64 = (a) kavdrate, apoi „o“ este rădăcina șaizeci și patru. Se împlinește opt ani. Răspuns: opt centimetri pătrați.

În cazul în care decizia rădăcină pătrată este în afara domeniului de aplicare al pătratelor din tabel, iar răspunsul nu funcționează în ansamblu, a salva calculatorul. Chiar și în aparatul cel mai simplu poate fi găsit sub valoarea rădăcină al doilea grad. Pentru a face acest lucru, tastați următorul set de butoane: „numărul“, care exprimă expresia radicală și „semn rădăcină.“ Raspuns pe ecran și va Podkoren valoare.

Dacă știți zona pătrat, în scopul de a găsi partea a pieței, este necesar să se ia rădăcina pătrată din valoarea numerică a zonei (din zona pătrat este egală cu pătratul mâna lui):
a = √S, în care
o - lungime laterală a unui pătrat;

S - zona de pătrat.
Unitatea de măsură a pătratului va fi unitatea liniară de lungime corespunzătoare măsurării ariei unității. De exemplu, în cazul în care suprafața pătrat este dat în centimetri pătrați. atunci lungimea sa laterală va centimetri doar.
exemplu:
pătrat zona de 9 metri pătrați.

Găsiți lungimea laturilor pătrat.
soluţie:
a = √9 = 3
răspundă:
parte a pătrat este egală cu 3 metri.

În cazul în care un perimetru pătrat cunoscut pentru determinarea lungimii laturilor perimetrului au nevoie de o valoare numerică împărțită la patru (din pătrat are patru laturi de lungime egală):
a = P / 4, în cazul în care:
o - lungime laterală a unui pătrat;

P - perimetrul pătrat.
Unitatea dintre laturile pătratului va fi aceeași unitate liniară de lungime cât și la perimetrul. De exemplu, în cazul în care perimetrul pătrat este dat în centimetri, atunci lungimea sa laterală a obține, de asemenea, în centimetri.






exemplu:
Perimetrul pătrat este de 20 metri.

Găsiți lungimea laturilor pătrat.
soluţie:
a = 20/4 = 5
răspundă:
Lungimea pătrat este egală cu 5 metri.

Dacă știm lungimea diagonalei unui pătrat, lungimea laturilor sale să fie egală cu lungimea diagonalei sale, împărțit la rădăcina pătrată a 2 (teorema lui Pitagora, ca laturile adiacente ale unui pătrat și diagonala unui triunghi isoscel dreptunghiular):
a = d / √2

(Ca ^ 2 + a ^ 2 = d ^ 2), în cazul în care:
o - lungime laterală a unui pătrat;

d - lungimea diagonalei pătratului.
Unitatea dintre laturile pătratului va fi unitatea de lungime este aceeași cu cea a diagonalei. De exemplu, dacă diagonala unui pătrat se măsoară în centimetri, iar lungimea laturilor sale va fi în centimetri.
exemplu:
Diagonalei pătratului este de 10 de metri.

Găsiți lungimea laturilor pătrat.
soluţie:
a = 10 / √2 sau despre: 7.071
răspundă:
Lungimea pătrat este egală cu 10 / √2, sau aproximativ 1071 de metri.

„Ecuația“ în matematică se numește o înregistrare care conține unele operații matematice sau algebrice și implică în mod necesar un semn egal. Cu toate acestea, de multe ori acest concept nu indică identitatea întregului, dar numai partea stângă. Prin urmare, sarcina de construcție a ecuației în piața implică cel mai probabil, utilizarea acestei operațiuni numai la monom sau un polinom în partea stângă.

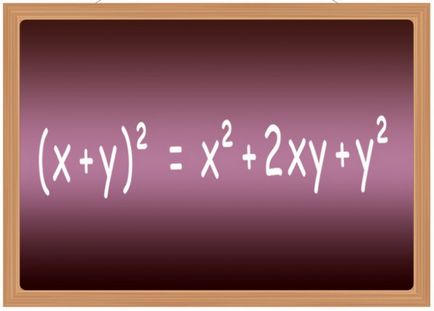
Înmulțiți ecuația de la sine - aceasta este construirea unei operațiuni în al doilea grad, care este, la pătrat. Dacă expresia originală conține variabile în orice grad, exponentul trebuie crescută de două ori. De exemplu, (4 Xg *) ² = (4 * Xg) * (4 * Xg) = 16 * x⁶. Dacă este prezent în ecuația coeficienților numerice multiplicat în mintea lui nu este posibil, folosiți calculatorul de calculator on-line sau o fac pe hârtie „o coloană.“

În cazul în care expresia inițială conține mai multe variabile adunare sau scădere cu coeficienți numerice (de exemplu, este un polinom), trebuie să efectueze multiplicarea normelor relevante. Acest lucru înseamnă că este necesar să se multiplice fiecare termen al ecuației -mnozhimogo pe fiecare membru este un factor al ecuației, și apoi simplifica expresia rezultată. Faptul că, în cazul dumneavoastră cele două ecuații sunt aceleași, nu se schimbă nimic în această regulă. De exemplu, dacă este necesar să pătrat ecuația x² + 4-3 * x, întreaga operațiune poate fi scrisă sub forma: (x² + 4-3 * x) ² = (x² + 4-3 * x) * (x² + 4 -3 * x) = x⁴ + 4 * x²-3 * Xg + 4 * x² + 16-12 * x - 3 * Xg-12 * x + 9 * x². Expresia rezultată trebuie să fie simplificate și, dacă este posibil, așezați termenii de putere în ordinea exponentului descrescătoare: x⁴ + 4 * x²-3 * Xg + 4 * x² + 16-12 * x - 3 * Xg-12 * x + 9 * x² = x⁴ - 6 * Xg + 25 * x² - 24 * x + 16.

Formula Cuadratura unele expresii comune mai bine să memoreze. La școală, ele includ de obicei o listă numită „formule de multiplicare prescurtate.“ Aceasta se referă, în special, cu formula erecției doua sumă grad de două variabile (x + y) ² = x² + 2 * x * y +, diferența lor Ya (xy) ² = x²-2 * x * y + Ya, suma trei componente (x + y + z) ² = x² + Ya + z² + 2 * x * y + 2 * y * z + 2 * x * z și diferența de trei termeni (xyz) ² = x² + Ya + z²-2 * x * y + 2 * x * y-2 * z.