Partea 1 din 4: Calcularea probabilității unei unități de Editare eveniment aleator
Se determină numărul de evenimente posibile și rezultate. Probabilitatea - raportul dintre posibila apariție a uneia sau mai multor evenimente la numărul total de rezultate posibile. De exemplu, doriți să aflați cum pierderea probabilă a trei să moară cu șase laturi. „Pierderea Trei“ - un eveniment, și 6 - numărul de rezultate posibile. Iată câteva exemple pentru a vă ajuta să înțelegeți:
- Exemplul 1: Care este probabilitatea de a alege o zi liberă, alegând accidental numărul?
- „Alegerea week-end“ - un eveniment, iar numărul de opțiuni egal cu numărul de zile într-o săptămână - șapte.
- Exemplul 2. Banca lăptișor 4 este albastru, roșu și 5 11 bile albe. Dacă presupunem că bilele sunt amestecate și sunt trase la întâmplare, ceea ce este probabilitatea de a extrage un roșu?
- „Trageți roșu“ - acest eveniment, precum și numărul de rezultate posibile este egal cu numărul de bile în bancă 20.
Se împarte numărul de evenimente dorite de numărul total de evenimente posibile. Vei primi o probabilitate de apariție a unui singur eveniment. În cazul pierderii trei pe zaruri (în zaruri doar un triplu), probabilitatea poate fi exprimată ca 1 ÷ 6, 1/6, 0,166, sau 16,6%. Iată câteva exemple de calcul a probabilității pentru alte exemple:
- Exemplul 1: Care este probabilitatea de a alege o zi liberă, alegând accidental numărul?
- Din moment ce va fi de 2, iar numărul de evenimente posibile este 7. Probabilitatea va fi de 2 ÷ 7 = 2/7, sau 0,285 sau 28,5% în săptămâna, două zile libere, numărul de evenimente dorite.
- Exemplul 2. Banca lăptișor 4 este albastru, roșu și 5 11 bile albe. Dacă presupunem că bilele sunt amestecate în sus și scos la întâmplare, ceea ce este probabilitatea de a extrage un roșu?
- Numărul de evenimente dorit este egal cu numărul de bile roșii în bancă - 5, numărul total de evenimente este 20. Probabilitatea de 5 ÷ 20 = 1/4, sau 0,25, sau 25%.
Partea a 2 din 4: Calcularea probabilității setului de evenimente aleatoare Editare
Se împarte problema în părți. Calcularea probabilității unui set de evenimente constă în calcularea probabilității mai multor evenimente individuale. Iată câteva exemple:
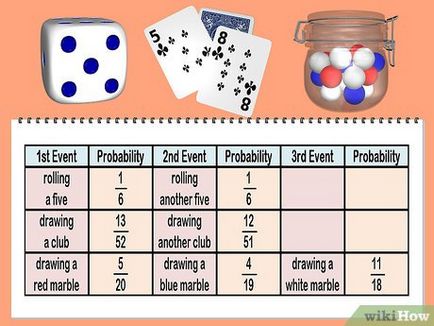
- Exemplul 1: Care este probabilitatea ca zarurile vor cădea de două ori numărul cinci?
- După cum știm deja, probabilitatea de numărul cinci este 1/6, iar probabilitatea de-al doilea număr de cinci și 1/6.
- Aceste evenimente nu sunt legate, adică independente. pentru că puteți arunca zarurile de multe ori la rând, iar acest lucru nu va afecta condițiile inițiale.
- EXEMPLUL 2: Două cărți sunt scoase de pe punte la întâmplare. Care este probabilitatea ca ambele cărți sunt de cluburi?
- Probabilitatea ca prima carte de cluburi - 13/52 sau 1/4, ca într-un pachet de 13 cărți în fiecare costum. Și probabilitatea de a extrage o a doua carte de cluburi vor avea 12/51.
- Tu calcula probabilitatea de evenimente conexe. Primul eveniment afectează al doilea; dacă ai trage 3 cluburi și puneți-l înapoi în punte, punte va fi unul dintre cluburile carte mai mici și mai mult de o carte din pachet (51 în loc de 52).
- Exemplul 3. In Bank 4 albastru, roșu și 5 11 bile albe. Dacă obțineți 3 mingi consecutive, ceea ce este probabilitatea ca primul este roșu, celălalt albastru, iar al treilea este de culoare albă?
- Probabilitatea ca primul este de culoare roșie, este 5/20 sau 1/4. Probabilitatea ca al doilea albastru - 4/19, întrucât toate bilele va fi una mai puțin, dar numărul de albastru este redus. Probabilitatea ca un al treilea este de culoare albă, este 11/18, pentru că acum ai scos 2 bile. Acesta este un alt exemplu de evenimente conexe.
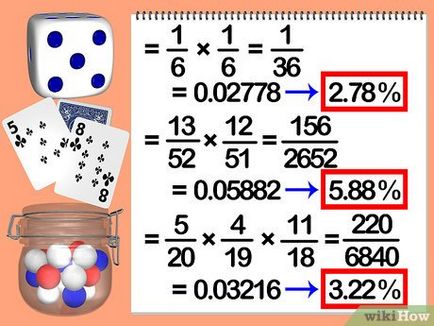

Înmulțiți probabilitățile împreună. Acest lucru vă va da probabilitatea ca evenimentele vor avea loc consecutiv. Iată ce trebuie să faci:
- Exemplul 1: Care este probabilitatea ca zarurile vor cădea de două ori numărul cinci?
- Astfel, obținem o 1/6 x 1/6 = 1/36 sau 0,027 sau 2,7%.
- EXEMPLUL 2: Două cărți sunt scoase de pe punte la întâmplare. Care este probabilitatea ca ambele cărți sunt de cluburi?
- Probabilitatea primului eveniment - 13/52. Probabilitatea de a doua - 12/51. Global probabilitate - 13/52 x 12/51 = 12/204 sau 1/17, sau 5,8%.
- Exemplul 3. In Bank 4 minge albastru, roșu și 5 11 alb. Dacă obțineți 3 mingi consecutive, ceea ce este probabilitatea ca primul este roșu, celălalt albastru, iar al treilea este de culoare albă?
- Probabilitatea de primul eveniment este 5/20, în al doilea rând - 4/19, al treilea - 11/18. probabilitate totală - 5/20 x 4/19 x 11/18 = 44/1368 sau 3,2%.