Calculul determinant matrice în ms Excel - compatibil cu Microsoft Excel 2018, Excel 2018

Calculăm determinanți (determinanți) ale matricei prin MDETERM () sau engleză. MDETERM, descompunere pe rând / coloană (3 x 3) și definiția (până la 6 ordine de mărime).

Determinantul matricei (det) poate fi calculată pentru matrici pătrate numai, adică al cărui număr de rânduri este egal cu numărul de coloane.

Pentru a calcula determinant în MS Excel are o caracteristică specială MDETERM (). Argumentul funcției trebuie să specifice o referință la un grup de celule (o matrice) care conține elementele matricei (vezi. Exemplul de fișier).

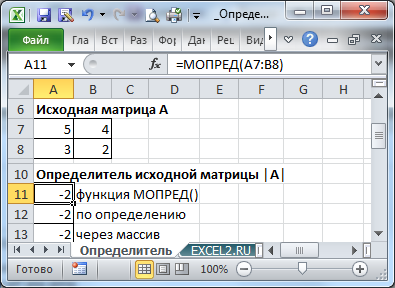
Matricea poate fi definit nu numai ca o serie de celule, cum ar fi A7: B8. dar, de asemenea, o serie de constante. de exemplu, MDETERM = (). Înregistrarea cu constantele de matrice nu permite indica elemente în celule individuale și puneți-le într-o celulă, împreună cu o funcție. Matricea în acest caz indicat prin linii: de exemplu, în primul rând, prima linie este de 5, 4, apoi prin colon următoarea linie se înregistrează 3; 2. Elementele sunt separate prin punct și virgulă.

Pentru matrici de ordinul 2 poate fi determinant poate fi calculată fără a utiliza funcția MDETERM (). De exemplu, pentru expresia de matrice de mai sus = A7 * B8-B7 * A8 va returna același rezultat.

Pentru o matrice de ordinul 3, plasat de exemplu în intervalul A16: C18. expresie complicată = A16 * (B17 * C18-C17 * B18) -B16 * (A17 * C18-C17 * A18) + C16 * (A17 * B18-B17 * A18) (expansiune într-un rând).

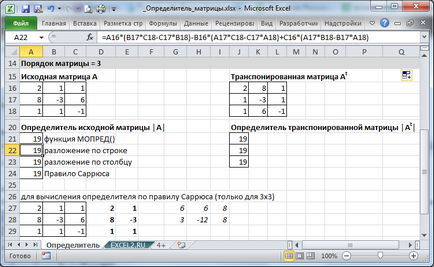
Exemplul de fișier pentru un determinant matrice 3 x 3 este de asemenea calculat prin descompunere pe coloană și regula Sarryusa.

proprietăți ale determinantului

Acum, unele dintre proprietățile determinantul (a se vedea exemplul de fișier.)

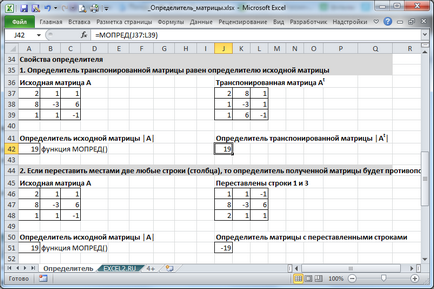
• Determinantul matricei este egal cu determinantul matricei transpuse inițial
• Dacă toate elementele într-o matrice de cel puțin unul dintre rânduri (sau coloane) sunt zero, determinantul acestei matrici este zero
• Daca swap două oricare rând (coloană), determinantul matricei rezultată este opusul originalului (adică, schimbarea semnului)
• Dacă toate elementele de un rând (coloana) este multiplicat cu același număr k, atunci determinantul matricei rezultat este egal cu determinantul matricei originale înmulțită cu k
  
• Dacă matricea conține rânduri (coloane), care sunt o combinație liniară a celorlalte rânduri (coloane), determinantul = 0
• det (A) = 1 / det (A-1), unde A -1 - matricea inversă a matricei A (A - matrice nesingular pătrat).

Calcularea determinantul definiției matricei (până la aproximativ 6 inclusiv)

După cum sa arătat mai sus, pentru a calcula matrici de ordine 2 și 3 sunt suficient de formule și regulamente simple. Pentru a calcula determinantul matricilor de ordin superior (fără MDETERM () funcția) va trebui să amintim definiția:

Determinant unei matrice pătrată de ordinul n × n este suma care conține n! termeni (= FACT (n)). Fiecare termen este produs n elementelor matricei, cu factor (-1) apare în fiecare produs conține un element din fiecare rând și din fiecare coloană a matricei A. Înainte de termenul k. în cazul în care elementele matricei A din produs, în ordinea numărului liniei și numărul de inversiuni din permutarea k din multitudinea de numere de coloane impare.

unde (a 1. α 2. αn) - permutare de numere întregi de la 1 la n. N (α 1. α 2. αn) - numărul de inversiuni din permutarea. însumarea trece peste toate permutarile posibile de ordinul n.

Noi încercăm să înțelegem această determinare complexă a matricei exemplu 3x3.

Pentru o matrice de 3 x 3, conform definițiilor, numărul termenilor este 3! = 6 și fiecare termen al produsului este format din 3 elemente ale matricei. 6 prezintă toți termenii necesari pentru calcularea determinantul matricei 3x3:

A21, A12, etc. - elementele matricei. Acum, să ne explice modul în care s-au format indicii ale elementelor, adică, de ce, de exemplu, există un termen a11 * A22 * a33 și a11 * nu * A22 A13.

Priviți formula de mai sus (a se vedea. Detection). Să presupunem că a doua subscriptului a fiecărui element al matricei (de la 1 la n) a matricei corespunde unui număr de coloană (deși poate fi numărul rândului (acest lucru nu este important, deoarece determinanții matricei și matricea transpusa sunt egale). Astfel, al doilea indice de primul element din produs este întotdeauna 1, al doilea - 2, 3. Apoi a treia primii indici ai elementelor corespund numărului liniei, și în conformitate cu definiția, trebuie determinată prin permutarea numere întregi de la 1 la 3, adică, setul de permutări (1 , 2, 3).

Acum înțeleg de ce există a11 * * A22 A13 printre termeni, deoarece conform definițiilor (conținute în fiecare element de lucru din fiecare rând și fiecare coloană a matricei A), iar în acest termen nici un element de linia 3.

Notă. Permutare setului de numere n (fără repetiții) este orice ordonare de seturi diferite unul de altul numai în ordinea elementelor lor constitutive. De exemplu, având în vedere un set de numere de 3: 1, 2, 3. Din aceste numere pot fi 6 permutări diferite: (1, 2, 3), (1, 3, 2), (2, 3, 1), ( 2, 1, 3), (3, 1, 2), (3, 2, 1). A se vedea Permutări articol fără repetarea :. combinatorică în MS Excel

Numărul de permutări ale unui set de 3 numere = 3! = 6 (care, desigur, egal cu numărul de termeni în expresia pentru calcularea determinantului, deoarece fiecare termen corespunde unui alt permutare). Pentru o matrice de 3x3 toate permutările sunt prezentate în nota de mai sus. Se poate observa că, în fiecare termen a primelor indicii ale elementelor sunt egale cu numerele corespunzătoare din permutarea. De exemplu, la a21 * a12 * a33 Termenul permutare folosit (2, 1, 3).

TIP. Pentru o matrice de ordinul 4 sunt 4! permutări, adică 26, ceea ce corespunde termen de 26, fiecare dintre acestea fiind un produs al diferitelor elemente ale matricei 4. Toate cele 26 de permutări pot fi găsite în căutarea tuturor permutări posibile în MS Excel.

Acum, când sortate cu termeni care definesc factorul înainte de fiecare termen (care poate fi +1 sau -1). Factorul este determinat de numărul de inversiuni paritate permutare corespunzătoare.

Notă. Inversiunea permutărilor (și paritatea numărului de inversiuni) pot fi citite, de exemplu, în permutarile articol fără repetiție: combinatorică în MS EXCEL

De exemplu, primul termen corespunde permutare (2, 1, 3), în care inversiune este 1 (număr impar) și, în mod corespunzător, în măsura -1 1 -1. Al doilea termen corespunde permutare (2, 3, 1), în care cele două inversiuni (chiar și număr), și în consecință, -1 este egal cu 1 grad 2, etc.

Rezumând toți termenii: (-1) * (a21 * a12 a33 *) + (+ 1) * (a21 * a32 a13 *) + (- 1) * (a11 * a32 a23 *) + (+ 1) * (a11 * a22 a33 *) + (- 1) * (a31 * a22 a13 *) + (+ 1) * (* a31 a12 * a23) obținem valoarea determinantului.

În exemplul 4+ fișier pe foaie și ordinea Edit matrice prin control contor. putem calcula determinantul ordinii de până la 6 inclusiv.

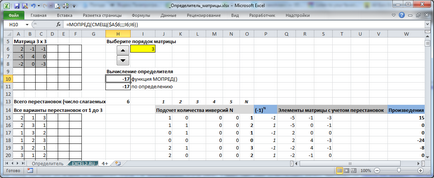
Trebuie amintit că calcularea matricei de ordine 6 în expresia a fost folosit 720 termeni (6!). Pentru ordinul 7-lea ar trebui să facă o masă pentru 5040 și permutări, respectiv, pentru a calcula 5040 termeni! Ie fără MDETERM () nu face (bine, sau puteți calcula manual determinant prin Gauss).