Volumul piramidei - formula, un exemplu de calcul
Chemat poliedru piramidă a cărei bază este poligon arbitrar, și toate fețele sunt triunghiuri cu un nod comun, care este un vârf al piramidei.
Pyramid - o cifră de volum. De aceea, pe care doriți să găsiți este de multe ori nu numai zona, ci și volumul. Formula pentru volumul piramidei este foarte simplu:
unde S - suprafața de bază, și h - înălțimea piramidei.
Înălțimea piramidei este numit direct, a scăzut de la summit-ul său de la baza la un unghi drept. Prin urmare, în scopul de a găsi volumul piramidei, trebuie sa determine care poligon se află la baza, se calculează suprafața sa, găsiți înălțimea piramidei și de a găsi volumul său. Luați în considerare exemplul de calcul al volumului unei piramide.
Sarcina a fost dat o piramidă patrulateră regulată.
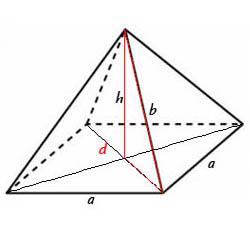
Baza laterale a = 3 cm, toate muchiile laterale b = 4 cm. Găsiți volumul piramidei.
Pentru a începe, să ne amintim că, pentru a calcula înălțimea volumului necesar al piramidei. Putem găsi în teorema lui Pitagora. Pentru aceasta avem nevoie de lungimea diagonală - sau mai degrabă jumătate din ea. Apoi, cunoscând două dintre laturile unui triunghi dreptunghic, putem găsi înălțimea. Pentru a începe, găsiți o diagonală:
Înlocuind valori în formula:
Înălțimea h, vom găsi cu ajutorul d b și nervurile:
Acum vom găsi zona pătrat. care se află la baza unei piramide regulate:
Substituind valorile obținute în formula de calcul a volumului:
Așa, cunoscând proprietățile piramide și mai multe formule, putem calcula volumul său.
- Zona piramidei hexagonale
- Zona de piramidă triunghiulară
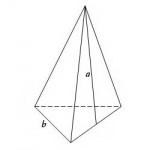
- Zona piramidei patrulater
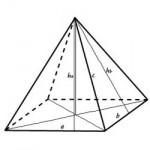
- Aria suprafeței laterale a piramidei
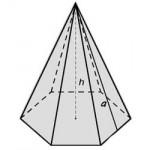
- Volumul piramidei hexagonal