unghiuri centrale și înscris într-un loc de muncă 6
Astăzi ne uităm la un alt tip de activitate 6 - de data aceasta cu un cerc. Mulți studenți nu le place și se pare dificil. Și este în zadar, pentru că aceste sarcini sunt simple. dacă știți că unele dintre teoremei. Sau nu pot fi rezolvate la toate, dacă ei nu știu.
Înainte de a vorbi despre proprietățile de bază, să ne amintim definiția:
Unghiul Inscripționată - unul al cărui vârf se află pe cercul în sine, iar partea tăiată pe o coardă a cercului.
Unghiul central - este orice unghi cu vârful în centrul cercului. partea lui se intersectează, de asemenea, acest cerc și se taie pe coardă ei.
Deci, conceptul de unghiurile inscriptionare centrale sunt indisolubil legate de cerc și o coardă în ea. Și acum - afirmația de bază:
Teorema. Unghiul central este întotdeauna de două ori inscripționată, bazată pe același arc.
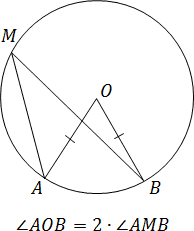
În ciuda simplității declarației, există o întreagă clasă de probleme 6, care poate fi rezolvată prin folosirea ei - și nimic altceva.
Sarcină. Localizați unghi inclus acut, bazat pe o coardă egală cu raza cercului.
Să AB - considerată coardă, O - centrul cercului. construcții suplimentare: OA și OB - razele cercului. obținem:
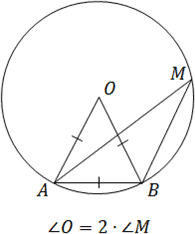
Luați în considerare triunghiul ABO. Acesta AB = OA = OB - toate laturile egale cu raza cercului. De aceea ABO triunghi - echilateral, și toate colțurile l cu 60 °.
Fie M - partea de sus a unghiului înscris. Deoarece unghiurile O și M se bazează pe același arc AB. Unghiul care include M de 2 ori mai mic unghi centrale O. Avem:
M = O. 2 = 60. 2 = 30
Sarcină. Unghiul central 36 ° mai mult decât unghiul inscris subîntins de acelasi arc circular. Găsiți unghiul înscris.
- AB - coardă a cercului;
- Punctul O - centrul cercului, astfel încât unghiul AOB - centru;
- Punctul C - vârf inscripționată unghi ACB.
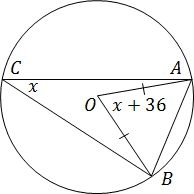
Din moment ce sunt în căutarea inscripționate unghiul ACB. notat cu x = ACB. Apoi unghiul AOB central este x + 36. Pe de altă parte, dintr-un unghi central de 2 ori mai circumscrisă. Avem:
AOB = 2 · ACB;
x + 36 = 2 · x;
x = 36.
Aici vom găsi inscripționată unghi AOB - este egal cu 36 °.
Circumferința - este unghiul de 360 °
Dupa ce a citit subtitrarea, cititorii informați vor spune acum, „Ugh!“ Și, într-adevăr, în comparație cu unghiul cercului nu este în întregime corectă. Pentru a înțelege ce vreau să spun, să ia o privire la cercul trigonometric clasic:

De ce această imagine? Iar faptul că o revoluție completă - unghiul de 360 de grade. Și dacă îl împărțiți de, să zicem, 20 de părți egale, dimensiunea fiecăreia dintre ele va fi de 360 de grade 20 = 18. Aceasta este ceea ce este necesar pentru a rezolva problema B8.
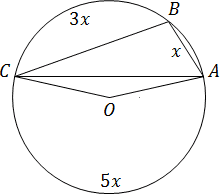
Punctul A. B și C sunt pe un cerc și împărțiți-l în trei arce de cerc, măsuri de gradul care sunt ambele 1. 3. 5. Localizați un unghi mai mare al triunghiului ABC.
Pentru a începe, găsiți măsura fiecărui grad arc. Să mai mică dintre ele egală cu x. Cifra indicată de arcul AB. Apoi, restul de arc - BC și AC - pot fi exprimate prin intermediul AB. arc BC = 3 x; AC = 5 x. Împreună, acestea oferă un arc de 360 de grade:
AB + BC + AC = 360;
x + 3, x + 5, x = 360;
9, x = 360;
x = 40.
Acum ia în considerare marele arc de curent alternativ. care nu conține punctul B. Acest arc drept corespunzător unghiului AOC central. egală cu 5 x = 5 x 40 = 200 de grade.
Unghiul ABC - cea mai mare dintre toate unghiurile unui triunghi. Acesta este înscris unghi, bazat pe același arc ca unghiul AOC central. De aceea, unghiul ABC 2 ori mai puțin AOC. Avem:
ABC = AOC. 2 = 200. 2 = 100
Acest lucru va fi măsura gradul de unghiul mai mare în triunghiul ABC.
Cercul circumscris despre un triunghi dreptunghic
Aceasta Teorema multe uita. Și în zadar, pentru că unele sarcini fără B8 nu a îndrăznit. Mai precis, ezitant, dar cu volumul de calcule pe care le va adormi mai degrabă decât ajunge la răspunsul.
Teorema. Centrul cercului circumscris despre un triunghi dreptunghic, se află în mijlocul ipotenuzei.
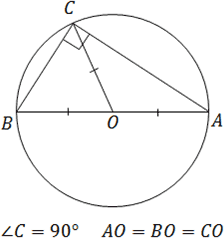
Ceea ce rezultă din această teoremă?
- Mijlocul ipotenuzei este echidistant față de toate vârfurile triunghiului. Aceasta este o consecință directă a teoremei;
- Mediana atras ipotenuzei împarte triunghiul original în două isoscel. Aceasta este exact ceea ce este necesar pentru a rezolva problema B8.
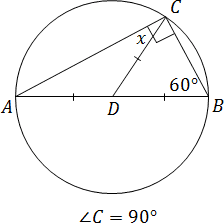
În triunghiul ABC, am realizat mediana CD-ul. Unghiul C este de 90 °, iar unghiul B - 60 °. Găsiți unghiul ACD.
Deoarece unghiul C este egal cu 90 °, ABC triunghi - dreptunghiular. Se pare că CD - mediana trase la ipotenuzei. Deci, ADC și triunghiul BDC - isoscel.
În special, considerăm ADC triunghi. Acesta AD = CD. Dar într-un triunghi echilateral, unghiurile de bază sunt egale - vezi „Sarcina B8: segmente și unghiuri în triunghiuri.“. Prin urmare, ACD = Un unghi dorit.
Astfel, rămâne pentru a afla ce este unghiul A. Pentru aceasta, ne întoarcem din nou la triunghiul inițial ABC. Notăm unghiul A = x. Deoarece suma unghiurilor în orice triunghi este de 180 °, avem:
A + B + BCA = 180;
x + 90 + 60 = 180;
x = 30.
Desigur, acesta din urmă problema poate fi rezolvată într-un alt mod. De exemplu, este ușor de a dovedi că triunghiul BCD - nu doar un isoscel și echilateral. Prin urmare, unghiul BCD este de 60 de grade. Prin urmare, unghiul ACD este de 90 - 60 = 30 de grade. După cum puteți vedea, puteți utiliza diferite triunghiuri isoscele, dar răspunsul va fi întotdeauna același.
- Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
