Rădăcinile ecuației trigonometrice în intervalul

13. 3-4cos rezolva ecuația 2 x = 0. Găsiți suma rădăcinile sale, aparținând intervalului [0; 3π].

Coborâți cosinusul prin formula: 1 + cos2α = 2cos 2 a. Noi obținem ecuația echivalentă:

3-2 (1 + cos2x) = 0 ⇒ 3-2-2cos2x = 0 ⇒ -2cos2x = -1. Impartim ambele părți prin (-2) și de a primi o ecuatie trigonometric simplu:

14. Găsiți b5 exponențial dacă b4 = 25 și b6 = 16.

Fiecare membru al unei progresie geometrică, începând cu a doua, egală cu media aritmetică a statelor membre vecine:

15. Găsiți derivata funcției: f (x) = tgx-ctgx.

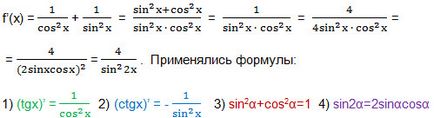
16. Găsiți valorile minime ale funcției y maxime și (x) = x 2 -12x + 27

Pentru a găsi valorile maxime și minime ale funcției y = f (x) în intervalul [a; b], pentru a găsi valorile acestei funcții la punctele finale și la punctele critice, care aparțin unui anumit segment, atunci toate valorile primite pentru a selecta maxim și minim.

Noi găsim valorile funcției x = 3 și x = 7, adică, la punctele finale.

y (3) = -12 ∙ 2 martie 3 + 27 = 9-36 + 27 = 0;

y (7) = -12 ∙ luna februarie 7 7 + 27 = 49-84 + 27 = -84 + 76 = -8.

Gasim derivata funcției: y '(x) = (x 2 -12x + 27)' = 2x-12 = 2 (x-6); punct critic x = 6 aparține unui interval dat [3; 7]. Găsim valoarea funcției la x = 6.

y (6) = -12 ∙ luna februarie 6 6 + 27 = 36-72 + 27 = -72 + 63 = -9. Acum alege din cele trei valori măsurate: 0; -8 -9 și cel mai mare și cel mai mic: unaib. = 0; unaim. = -9.

17. Găsiți forma generală a primitivelor pentru o funcție:

Acest decalaj - acesta este domeniul funcției. Răspunsurile trebuie să înceapă cu F (x), și nu cu f (x) - pentru că noi căutăm un primitiv. Prin definirea funcției F (x) este o primitivă pentru funcția f (x), în cazul în următoarea ecuație: F „(x) = f (x). Deci, puteți găsi cu ușurință derivata răspunsurilor propuse, până la o anumită funcție. O soluție riguroasă - un calcul al integralei funcției. Aplicăm formula:

19. Ecuația Marca liniei care conține mediana triunghiului ABC BD dacă nodurile sale A (-6, 2), B (6, 6) C (2; -6).

Pentru trasarea unei linii drepte a ecuației trebuie să știți coordonatele 2 puncte pe această linie, și știm doar coordonatele punctului B. Ca median al BD divide partea opusă în jumătate, punctul D este punctul de mijloc al segmentului de curent alternativ. Coordonatele punctului de mijloc jumătății sumei au coordonatele obiective. Găsim coordonatele punctului D.

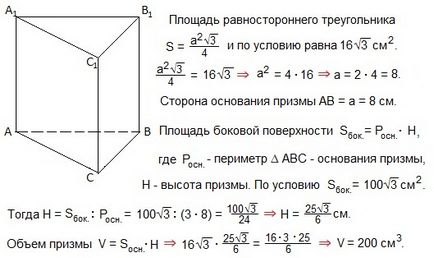
24. Zona unui triunghi echilateral, situată la baza unei prisme drepte, este

Această problemă - inversă problemă № realizare 24 de 0,021.

25. Găsiți un model și introduceți numărul lipsă: 1; 4; 9; 16; ...

Evident, acest lucru este numărul 25 așa cum ni se dă o secvență de pătrate de numere naturale:

01 februarie; 02 februarie; 02 martie; 02 aprilie; 02 mai; ...

noroc Toate bune și succes!