Probabilitatea de 10

Media raspredelenie.Funktsiya distribuție normală. Funcția Laplace. Caracteristici numerice ale distribuției normale. Probabilitatea de a lovi o variabilă aleatoare distribuită în mod normal, într-un anumit interval. de regulă cu trei sigma. Distribuțiile legate la normal: distribuția Student, și Fisher Pierce. Funcția caracteristică a distribuției normale.

8.1. Funcția de distribuție normală

Una dintre cele mai comune distribuții este distribuția normală. Acesta joacă un rol important în teoria probabilităților și aplicațiile sale. Rolul fundamental jucat de distribuția normală, pentru că suma variabilelor aleatoare, cu o creștere a numărului de termeni la o ipoteze destul de largi să se comporte asimptotic normal (vezi. „Central Limit Teorema“).

Densitatea funcției normale de distribuție are forma

Funcția normală de distribuție are forma

De multe ori, cu toate acestea, în locul funcției de distribuție normală cu ajutorul funcției Laplace.

Fie a = 0,  = 1, obținem

O astfel de funcție se numește distribuția normală standard. Scriem această funcție în formularul de mai jos

.

Deoarece F0 (+ ) = 1, apoi prin simetrie, primul termen este egal cu 0,5, iar al doilea termen este funcția Laplace

.

De aici obținem egalitatea

în funcție de distribuția normală și funcția Laplace de legare.

Există tabele extinse pentru distribuția normală standard și funcția Laplace. Cu toate acestea, trebuie să se țină seama de faptul că, uneori, în loc de funcții în considerare utilizarea funcției

sau funcția de eroare

Notă. Deschiderea unei distribuții normale asociată cu numele Gauss și Laplace. în care a apărut pentru prima dată legătură cu investigarea teoriei erorilor și metoda celor mai mici pătrate. Prin urmare, distribuția normală este, de asemenea, numit distribuția Gauss, Laplace. sau pur și simplu o distribuție Gauss sau Laplace.

Găsim așteptarea unei distribuții normale:

.

.

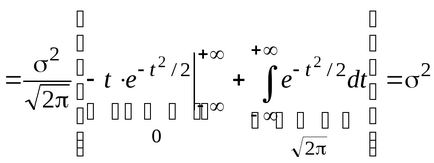
și anume Distribuția normală este caracterizată de doi parametri: a. având un sentiment de așteptare, și , având un sentiment al abaterii standard.

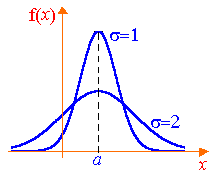
Graficul funcției normale de densitate de distribuție are următoarea formă (curba Gauss). Maximă este la x = a. puncte de inflexiune într-o a +  - și. Curba este simetrică în raport cu linia x = a. Odată cu scăderea  curba devine mai atins punctul culminant.

8.2. Probabilitatea de a lovi o variabilă aleatoare normal distribuită la un interval predeterminat

Este cunoscut faptul că, dacă variabila aleatoare X este definită de distribuție densitate f (x), probabilitatea ca X presupune valoarea aparținând intervalului (, ), are forma

.

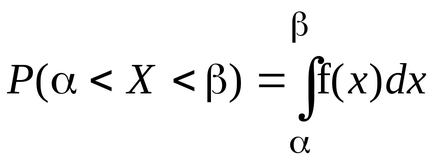
În cazul distribuției normale, această formulă ia forma următoare

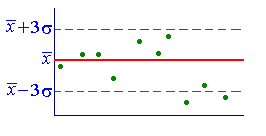
De multe ori este necesar pentru a calcula probabilitatea ca variabila aleatoare X deviația în valoare absolută mai mică decât un număr pozitiv predeterminat , adică este necesară pentru a găsi probabilitatea inegalitatea | X-a |<. Заметим, что неравенство равносильным ему двойным неравенством a –

.

În special, în cazul în care ,

Ultima egalitate arată că multe aspecte practice atunci când se analizează distribuția normală, putem neglija posibilitatea de deviere de la o variabilă aleatoare este mai mare decât 3 Acesta este așa-numitul regula „trei sigma“.

De exemplu, oricine este implicat în măsurători, sa întâlnit cu o situație în care există „o valoare sălbatică.“ În legătură cu această problemă: Excludeți valoarea, sau ar trebui să fie lăsat. Astfel, dezvoltarea de timp standard pentru fabricarea dintr-o bucată făcut următoarele măsurători: 5.0; 4.8; 5.2; 5.3; 5,0; 6.1. Ultimul număr este foarte diferit de alții. În acest sens, se pune întrebarea dacă eroarea este ascuns în măsurătorile aici. Se calculează valoarea medie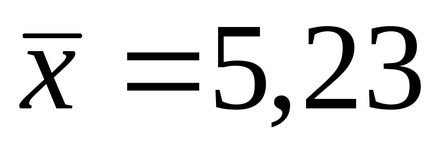

și pătrat medie otklonenie = 0,46. După acest interval vom construi „trehsigmovy“ (4,84; 6,61). Deoarece valoarea lui x = 6,1 nu se extinde dincolo de zona trehsigmovoy, aceasta nu poate fi considerată ca fiind „sălbatic“.

Un alt exemplu. Pe un transportor fabricat părți. Bazat pe elemente de monitorizare a datelor statistice medie calculată otklonenie pătrat. Apoi, să construiască o linie de mijloc directă, franjurate benzi trehsigmovoy. În cazul în care punctele de măsurători de control se află banda trehsigmovoy, procesul ar trebui să fie considerate ca fiind produse de înaltă calitate și stabile. În cazul în care punctele sunt aproape de liniile de ghidare, dar nu merg dincolo de zona trehsigmovoy, acest lucru indică proces discordie. Dacă punctul de dincolo de zona trehsigmovoy, aceasta înseamnă că există o căsătorie.

Exemplul 8.1. Masina produce bile. Mingea este considerat apt dacă diametrul bilei abatere X de proiectare a valorii absolute nu este mai mare de 0,7 mm. Presupunând că variabila aleatoare X este în mod normal distribuită cu o deviație standard de 0,4 mm. determina ce procent din disponibile bile produce mașină.

În consecință, aparatul produce 92% din piese adecvate.

8.3. Distribuția normală asociată cu

8.3.1. Distribuție Pearson ( 2 -Distribuitor)

Să variabile independente aleatoare U1. U2. ..., Uk descrie distribuția normală standard: Ui = N (0,1). Apoi, distribuirea sumei pătratelor acestor valori

Se numește  2 de distribuție ( "chi-pătrat") libertatea skstepenyami. În mod explicit, densitatea acestei funcții de distribuție are forma

unde

Funcția gamma; în special,  (n + 1) = n.

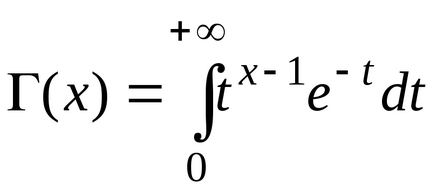
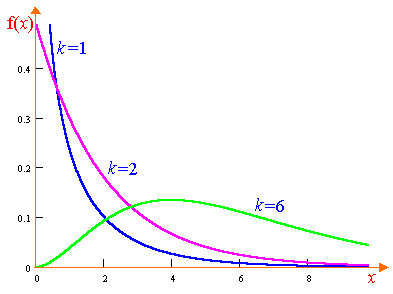
Pearson de distribuție este determinată de un singur parametru - numărul de grade de libertate k. Graficele acestei funcții sunt prezentate în Fig. 8.2. Caracteristici numerice ale distribuției Pearson:

În cazul în care variabilele aleatoare cPET 2 (k1) și  2 (k2) sunt independente, atunci

.

Rețineți că, odată cu creșterea numărului de grade de libertate de distribuție Pearson se apropie treptat normală.

8.3.2. distribuție Student (t-distribuție)

Să presupunem că U este un standard de variabile aleatoare normale, U = N (0,1), și  2 - variabila aleatoare cu  2 -Distribuitor cu k grade de libertate, în care U și cPET 2 variabile independente. Apoi, distribuția

Se numește distribuție (t-distribuție) libertatea skstepenyami Student. În mod explicit, densitatea funcției de distribuție Student are forma

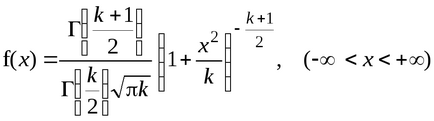
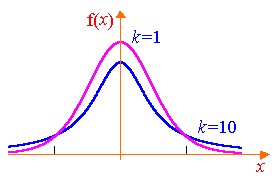
Graficul acestei funcții este prezentată în Fig. 8.3.

Caracteristici numerice ale distribuției Student:

Rețineți că, cu o creștere a numărului de grade de libertate de distribuție elevului se apropie rapid normală.

8.3.3. Distribuția de Fischer (F-distribuție)

Să  2 (k1) și  2 (k2) - variabile aleatoare independente având  2 -Distribuitor cu grade, respectiv, și k1 k2 de libertate. distribuirea

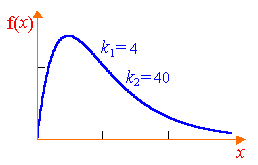
numita distribuție Fisher (F-distribuție) svobodyk1ik2 sostepenyami. Fisher densitatea de distribuție în mod explicit are forma

Graficul acestei funcții este prezentată în Fig. 8.4.

Caracteristici numerice ale distribuției Fisher:

TMemo că între variabile aleatoare cu o distribuție normală, distribuția Pearson, Student si Fisher, avem relații:

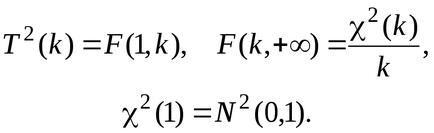
8.4 *. Funcția caracteristică a distribuției normale

Să  variabilă aleatoare distribuită prin distribuția normală standard. Apoi, vom obține pentru funcția caracteristică

.

Efectuarea de schimbarea y = x-it. obținem

.

Din teoria funcțiilor unei variabile complexe este cunoscut faptul că

.

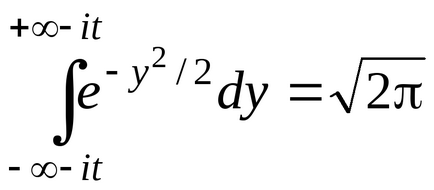
Prin urmare, vom obține în cele din urmă

.

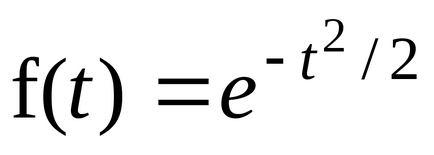
După cum am văzut, în cazul în care variabila aleatoare  distribuită prin distribuția normală standard, atunci variabila aleatoare  = t + m, dar distribuit legea normală cu parametrii m și . Apoi, caracteristici caracteristice f (t) și f (t) sunt legate de proprietatea 2 de relația

,

sau în cele din urmă obține că funcția caracteristică a distribuției normale este dată de