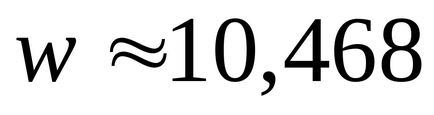mișcare complexă a unui punct

mișcare complexă a unui punct se numește mișcarea sa în raport cu sistemul de coordonate fix. Viteza și accelerația la punctul de circulație complexe notate

și și nazyvayutsyaabsolyutnoy iabsolyutnym accelerarea vitezei.

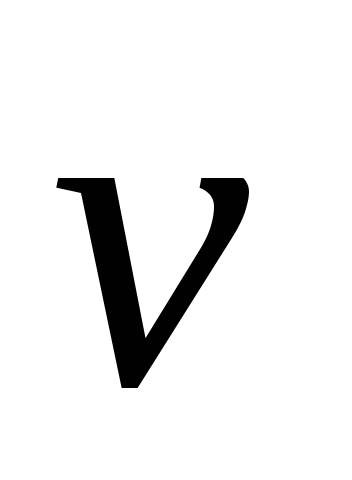
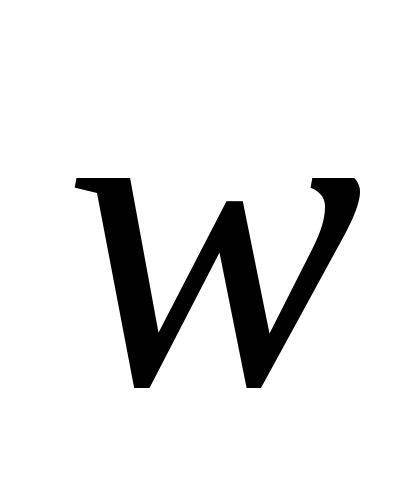
Mișcarea relativă a punctului se numește mișcarea sa în cadrul mișcare de referință, anumite mișcări în raport cu sistemul fix. Viteza și accelerația mișcării relative sunt notate

și și viteza nazyvayutsyaotnositelnoy și accelerația relativă.

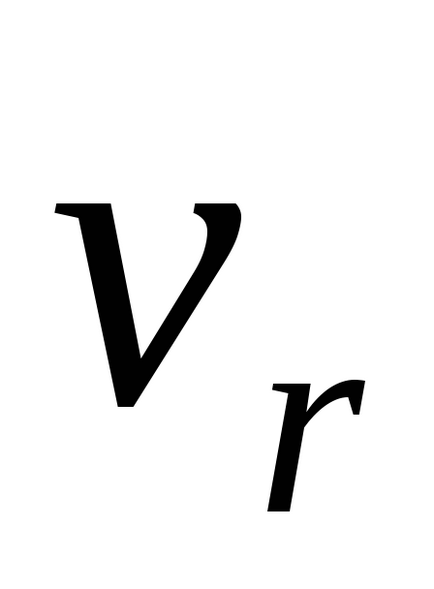
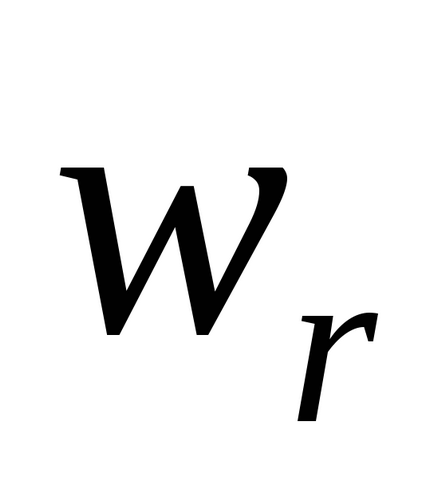
Punct de mișcare portabil se numește mișcare în raport cu un sistem de punct fix al cadrului de referință în mișcare cu care același punct la momentul respectiv. Viteza și accelerația mișcării de translație sunt notate

și și viteza nazyvayutsyaperenosnoy și accelerarea portabile.

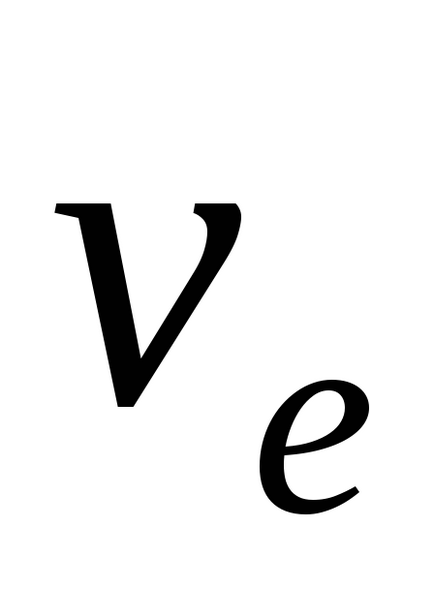
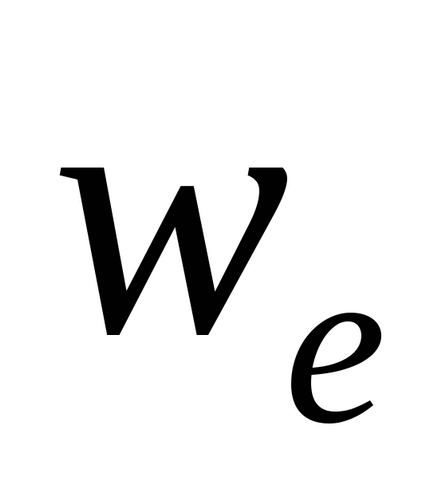
Viteza absolută a unui punct este egală cu suma geometrică a vitezei sale relative și portabil:

,

.

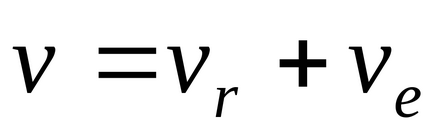
Punct de accelerație absolută este egală cu suma geometrică a accelerației relative, portabile și accelerația Coriolis, care este definită ca de două ori viteza unghiulară a produsului vectorial al vitezei relative mișcare de translație:

,

Direcția de accelerație Coriolis este convenabil pentru a găsi la regula Zhukovsky:

prin acest punct să dețină un plan perpendicular pe axa de rotație instantanee a portabilului;

proiectat pe acest plan de viteză relativă;

ducând la rândul său, construit planul de proiecție cu 90 ° față de axa de rotație instantanee în direcția portabilului.

Sarcina 4. Determinarea vitezei absolute și punctul de accelerație absolută în mișcarea complexă

Folosind starea lucrării de 3 și valorile găsite pentru punctele din timp

pentru a determina viteza absolută iar accelerația absolută cursoare. Având în vedere că el se mișcă pe plastinyAVS storoneAV. Poziția cursorului este determinat zakonomAM (t) = | AB | ∙ k (t). Datele solicitate se referă. Tabelul. 6.

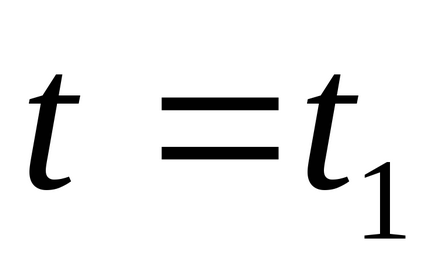
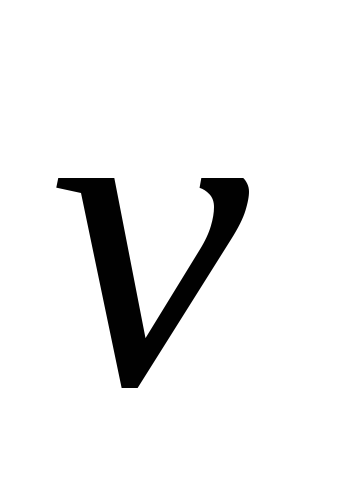
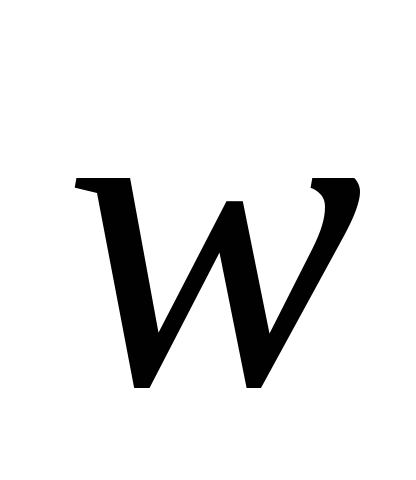
Dată: O1 (0; 0), O2 (11, 3), A (3, 0), B (9, 6) C (5, 4), D (2, 8), α = 90˚,

cu,





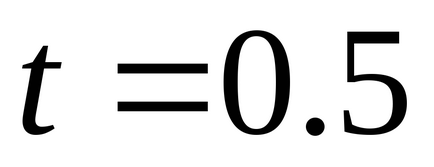
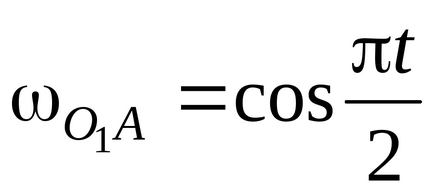
, cm.

Pentru a determina viteza absolută și punctul de accelerație absolută.

Mișcarea relativă a slide-M este mișcarea sa de-a lungul pryamoyAV.

Definiți poziția punctului M Naawi:

cm; vitezăcm / s și accelerațiacm / s 2 mișcare relativă. vectori de direcție și stabilit pe baza valorilor lor, trebuie să se țină seama de faptul că direcția pozitivă a mișcării relative a unui punct dintr-un punct în direcția punctului. și negativ - în direcția opusă.

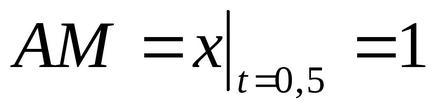
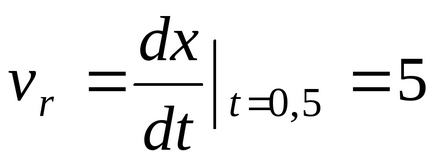
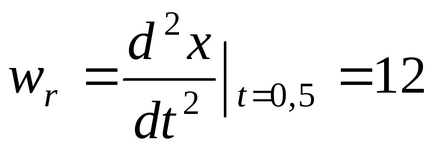
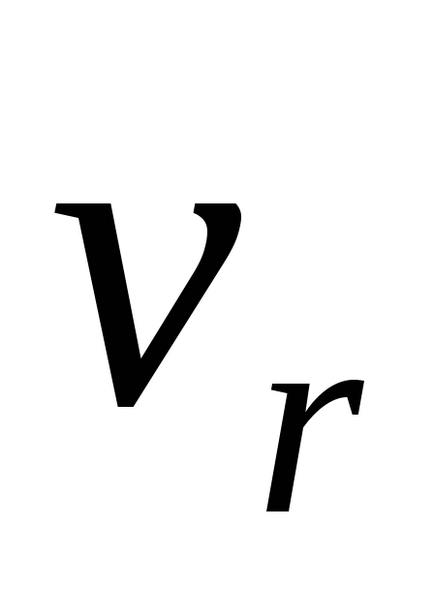
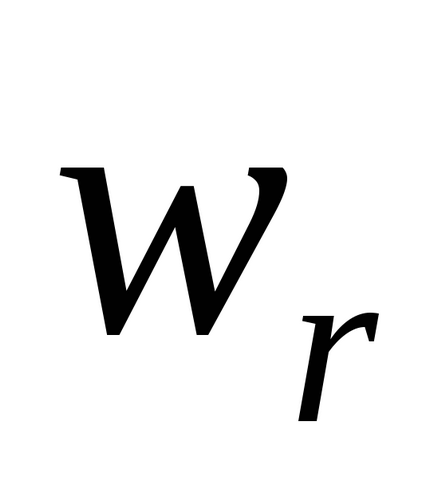
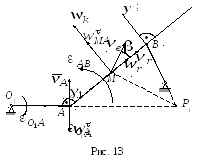
2. O mișcare portabilă

M mișcare de translație a cursorului este mișcarea pe plastineAVS sale de cale.

Viteza unghiulară și accelerația unghiulară a mișcării de translație, respectiv, viteza unghiulară egală și accelerația unghiulară placa ABC. și anume

și .

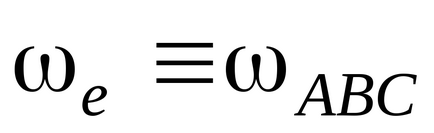
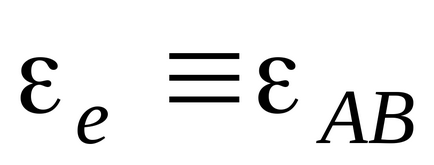
Pentru a determina viteza de translație

este necesar, folosind soluția la prima problemă, găsiți viteza de telaAVS puncte. situat pe storoneAV rasstoyaniiAM pe punct. În acest caz, punctul de viteză, sms :.

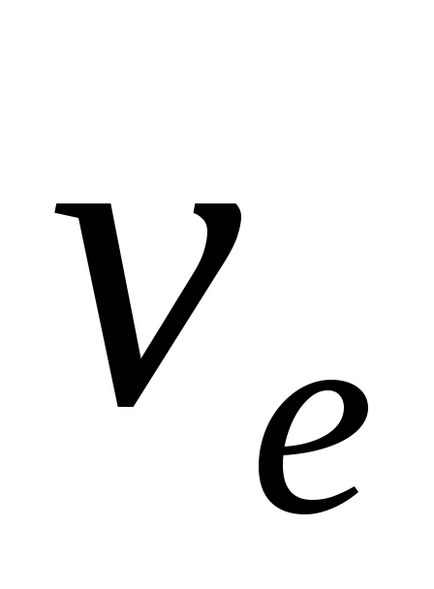
Valoarea accelerării portabile

De asemenea, coincide cu valoarea telaAVS punctului de accelerare. Prin urmare, vom defini relația:

.

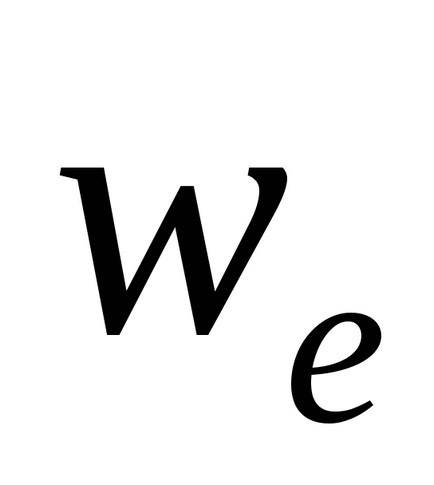
Proiectarea acest raport pe axa

și , prima dintre care este direcționat vdolAB. iar celălalt perpendicular pe acesta (figura 13), obținem proiecția unei accelerări portabile sms 2. pe aceste axe:

;

.

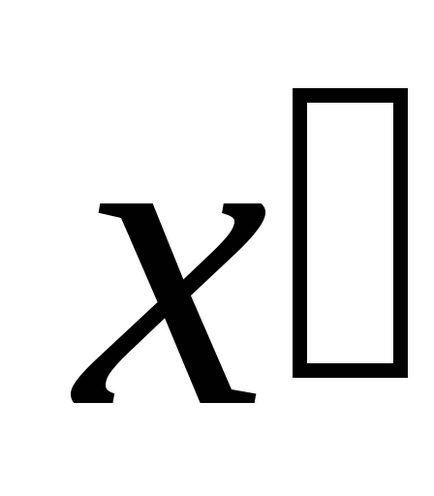
3. Accelerarea Coriolis

Definiți modulul accelerație Coriolis sms 2:

.

Direcția vectorului

arată, fie din definiția produsului vectorial a doi vectori, fie regula Zhukovskogo (Figura 13).

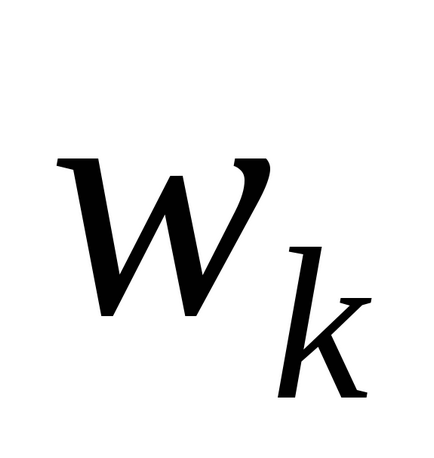
4.Absolyutnoe mișcare. mișcare absolută a cursorului - este de mișcare lui în raport cu sistemul otschetaxO1y fix. vector de viteză absolută este egală cu suma geometrică a vitezelor sale portabile și relative, iar modulul său este, sms:

,

unde

- unghiul dintre vectorii și , și poate fi găsit la treugolnikaAR1M Sines:

.

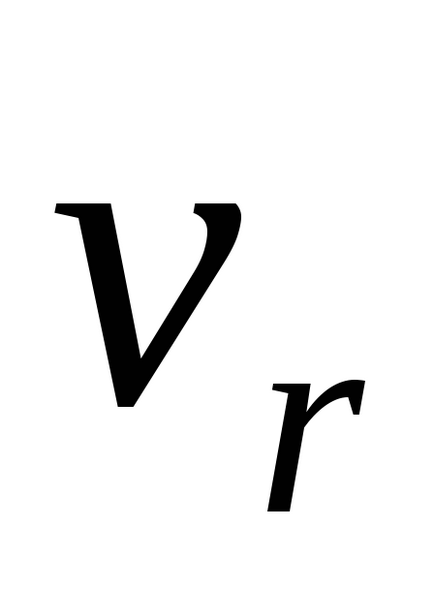
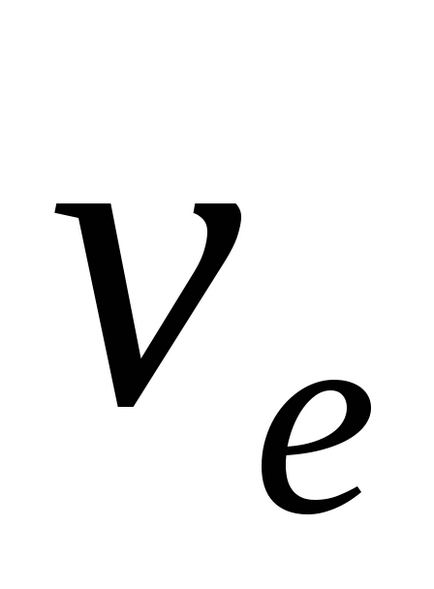
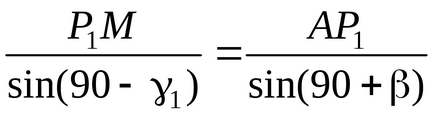
Pentru a determina proiectul de accelerare absolută a egalității vectorului pe axa

și , cm / sec 2,

;

.

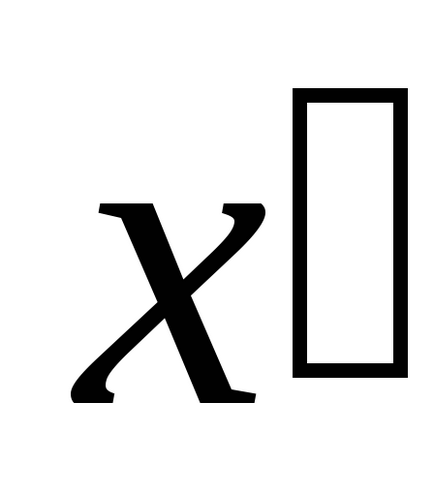
Astfel, valoarea absolută a accelerației

răspundă:

cm / s; cm / s 2.