Mediana la ipotenuzei triunghiuri

Mediana atras ipotenuzei este egal cu jumătate din ipotenuzei.

Având în vedere: Δ ABC, ∠ BCA = 90º

Demonstrati ca mediana atras ipotenuzei este egal cu jumătate din ipotenuzei.

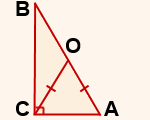
1) Într-un triunghi dreptunghic ABC din vârful drept unghiul C pentru a efectua segmentul AB CO ipotenuza, astfel încât CO = OA.

2) AOC Δ - bază isoscel AC (prin definiție a unui triunghi isoscel).

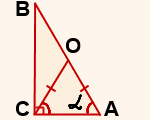
Prin urmare, unghiurile de la baza sunt: ​​∠ OAC = ∠ OCA = α.

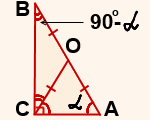
3) Deoarece suma colțurile ascuțite ale triunghiului dreptunghiular este egal cu 90 °, atunci triunghiul ABC ∠ B = 90º- α.

4) Deoarece BCA ∠ = 90º (prin ipoteză), apoi ∠ BCO = 90º- ∠ OCA = 90o-α.

5) Să BOC triunghi.

∠ BCO = 90o-α, ∠ B = 90º- α, prin urmare, ∠ BCO = ∠ B.

Deci, BOC - triunghi isoscel cu baza BC (pe baza unui triunghi isoscel).

6) Deoarece CO = OA (de construcție) și BO = CO (așa cum sa dovedit), CO = OA = BO, AB = OA + BO = 2 ∙ OA = 2 ∙ CO.

Astfel, punctul O - mijlocul ipotenuzei AB, segment CO conectează vârful triunghiului la mijlocul laturii opuse, apoi, CO - mediana trase la ipotenuzei și este egal cu jumătate din ipotenuza:

QED.

Această metodă poate fi utilizată pentru a demonstra proprietățile medianele unui triunghi dreptunghic în clasa a 7-a, din moment ce aceasta se bazează doar pe materialul deja cunoscut în momentul studierii subiectului.

O altă modalitate de a demonstra proprietățile mediana atras ipotenuzei, ia în considerare data viitoare.