Mediană a unui triunghi dreptunghic trase la ipotenuzei

Mediană a unui triunghi dreptunghic trase la ipotenuzei

Demonstrați că triunghiul înclinat median atras ipotenuzei este egal cu jumătate său.

Dovada unui tutore în matematică și fizică

Metoda I. construcție suplimentară.

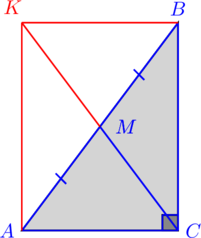
1. Desenați o linie dreaptă prin punctul paralel cu linia. Punctul de intersecție al acestei linii cu linia notată cu litera.

2. Apoi, așa cum sunt ele la cruce mint linii paralele și care se intersectează. De asemenea, din moment ce acestea sunt verticale. În plus, cu condiția. Prin urmare, de partea și adiacente la cele două colțuri ale lui.

3. Prin urmare. Asta este, cele două părți sunt egale și paralele în patrulaterul. Prin urmare, patrulaterul - un paralelogram. Mai mult decât atât, toate colțurile acestei paralelogram sunt drepte. În consecință, - un dreptunghi.

4. Aceasta este, deoarece este diagonala dreptunghiului. Mai mult, aceste bisect diagonal punctul de intersecție, prin urmare.

Metoda II. Descrie un cerc.

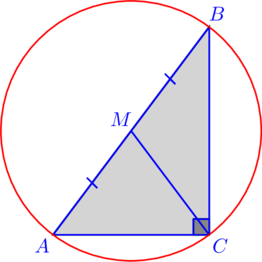
1. Descrie un cerc în jurul triunghiului. este diametrul cercului, deoarece - înscris în acest cerc și trebuie să se bazeze pe un semicerc.

2. Prin urmare, în cazul în care - raza cercului.

proces III. Soluția de rezolvare „până la sfârșit“.

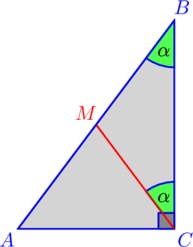
1. segment de tragerea la sorți, astfel încât. Apoi - isoscel, și, prin urmare.

2. În plus ,. În consecință, - isoscel, și, prin urmare.

3. Prin urmare. QED.