Lecția 3 matrice

Motorul nu se mișcă nava. Nava este încă în vigoare, iar motorul se mișcă universul în legătură cu acesta. Futurama

Aceasta este o parte foarte importantă a lecției, asigurați-vă că ați citit-o de mai multe ori și este bine înțeleasă.

Pana acum am operat o nodurile 3-dimensionale ca și (x, y, z) triplete. Vom introduce un alt parametru w și va opera pe vectori de forma (x, y, z, w).

Amintiți-vă întotdeauna că:

• Dacă w == 1, apoi vectorul (x, y, z, 1) - o poziție în spațiu.
• Dacă w == 0, vectorul (x, y, z, 0) - această direcție.

coordonate omogene ne permite, cu o singură formulă matematică pentru a opera cu vectori în ambele cazuri.

## Introducere în matricea

Cel mai simplu mod de a prezenta o matrice ca o serie de numere, cu un număr strict definit de rânduri și coloane. De exemplu, o matrice 2x3 după cum urmează:

Cu toate acestea, cele trei-dimensionale grafica, vom folosi doar o matrice 4x4, care ne va permite să transforme vârful nostru (x, y, z, w). Vârful transformat este rezultatul înmulțirii matricei pe foarte sus:

** Partea superioară a matricei x (în această ordine !!) = transformat. ** vertex

Destul de simplu. O vom folosi destul de des, asa ca are sens să-l încredințeze unui calculator:

Încercați să experimenteze cu aceste fragmente.

Matricea de transfer arată astfel:

în cazul în care X, Y, Z - valori pe care dorim să le adăugați la vectorul nostru.

Deci, dacă vrem să se mute vectorul (10, 10, 10, 1) la 10 unități în direcția X, atunci vom obține:

... obținem (20, 10, 10, 1) un vector omogen! Nu uitați că 1 în parametrul w, înseamnă poziția, dar nu și direcția, și transformarea noastră nu schimbă faptul că lucrăm cu poziția.

Acum, ia în considerare ceea ce se întâmplă în cazul în care vectorul (0, 0, -1, 0) este linia:

... și a obține vectorul nostru inițial (0, 0, -1, 0). Așa cum am menționat mai devreme, cu vectorul parametrului w = 0 nu poate fi transferat.

Și e timpul să-l mute în codul.

** În GLSL. ** De fapt, nu vei face în shader, de multe ori va efectua GLM :: translate () în C ++, pentru a calcula matricea, se transferă la GLSL, și deja în shader de a se multiplica:

Aceasta este o matrice specială, care nu face nimic, dar noi îl atinge, deoarece este important să ne amintim că A este înmulțit cu 1,0 dă A:

Se pare la fel de simplu:

Deci, dacă doriți să aplicați scalarea vectorului (poziția sau direcția - aceasta nu este important) la 2,0 în toate direcțiile, trebuie:

Rețineți că w nu se schimba, precum și să acorde o atenție faptului că matricea de identitate - este un caz special de scalare matrice cu un factor de scală de la 1 pentru toate axele. De asemenea, matricea de identitate - este un caz special al matricei de transfer, în cazul în care (X, Y, Z) = (0, 0, 0), respectiv.

Mai complicat decât cele considerate anterior. Noi omită detaliile aici, din moment ce nu trebuie să știe sigur pentru utilizarea de zi cu zi. Pentru mai multe informații, vă rugăm să faceți clic pe link-ul matricile și quaternions FAQ (resursa destul de popular și nu pot avea acces la limba dvs.)

## Alcătuirea transformarea

Deci, acum suntem capabili să se rotească, muta și scala vectorilor noștri. Următorul pas ar fi o idee bună de a combina transformarea care se realizează prin următoarea formulă:

ATENȚIE! Această formulă este, de fapt, arată că scalarea se realizează în primul rând, și apoi rândul său, și numai în ultimă instanță, dacă vă aflați în mișcare. Așa funcționează matrice de multiplicare.

Asigurați-vă că să-și amintească ordinea în care toate se face acest lucru, pentru că ordinea este foarte importantă în cele din urmă, îl puteți verifica-vă:

• Ia un pas înainte și virează la stânga
• Viraj stânga și să ia un pas înainte

Diferența este foarte important să se înțeleagă, pentru că va fi în mod constant confruntat cu aceasta. De exemplu, atunci când lucrați cu personaje de joc, sau unele obiecte, este întotdeauna mai întâi la scară, apoi rândul său, și apoi transferați.

Înmulțirea a două matrici este foarte asemănătoare cu multiplicarea matricelor și a vectorilor, astfel încât vom omite descrierea, și, dacă doriți să aflați mai multe, puteți să faceți clic din nou pe matricile link-ul și quaternions FAQ.

Până la sfârșitul acestui tutorial, vom presupune că știm cum să afișeze un model 3D al Blender tau preferat - Monkey Suzanne.

Mondială, specii și matricea de proiecție - este un instrument la îndemână pentru a împărți transformări.

Acest model, precum și triunghiul nostru roșu definit de setul de noduri ale căror coordonate sunt definite în raport cu centrul de obiect, adică coordonatele. E. Vertex (0, 0, 0) va fi în centrul obiectului.

În continuare, ne-ar dori să se mute modelul nostru, deoarece player-ul îl controlează folosind tastatura și mouse-ul. Tot ceea ce facem - este aplicat scalarea-l, atunci rotația și translația. Aceste acțiuni sunt efectuate pentru fiecare nod în fiecare cadru (realizată în GLSL, și nu în C ++!) Și, astfel, modelul nostru se mișcă pe ecran.

Acum nod nostru în spațiul mondial. Acesta arată săgeata neagră în figură. Ne-am mutat din obiect spatial (toate nodurile sunt definite în raport cu centrul obiectului) la spațiul internațional (toate nodurile sunt definite în raport cu centrul lumii)

Schematic, acest lucru este prezentat după cum urmează:

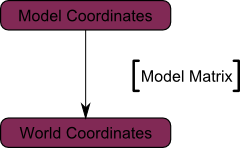
Încă o dată am citez Futurama:

Motorul nu se mișcă nava. Nava rămâne în același loc, iar motorul se mișcă universul în jurul lui.

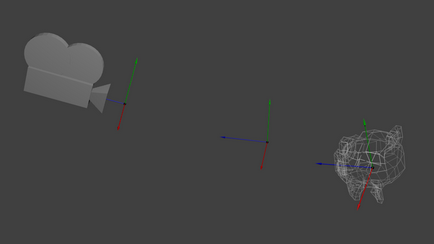
Încearcă să-l imagina în raport cu aparatul de fotografiat. De exemplu, dacă doriți să realizați fotografii ale muntelui, nu mișcați camera, și pentru a muta muntele. Nu este posibil în viața reală, dar este incredibil de simplu în grafica pe calculator.

Deci, inițial, camera foto este situat în centrul lumii sistemului de coordonate. Pentru a muta lumea, trebuie să se introducă o altă matrice. Să presupunem că doriți să mutați camera la 3 unități la dreapta (+ X), care este echivalentul a se deplasează în jurul lumii în 3 unități la stânga (-X). În codul, se pare ca acest lucru:

Din nou, imaginea completă de mai jos arată acest lucru. Ne-am mutat dintr-o lume de sistem (toate nodurile sunt definite în raport cu centrul sistemului mondial), coordonate la camera sistemul de coordonate (toate nodurile sunt definite în raport cu aparatul de fotografiat):

Ei bine, până când creierul îl digeră, ne uităm la funcția, care ne oferă GLM, ci mai degrabă pe GLM :: lookat:

Aici este o diagramă care arată ceea ce facem:

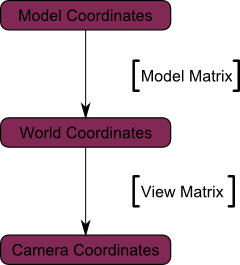
Deci, acum suntem în spațiul camerei. Acest lucru înseamnă că, în partea de sus a care vor primi coordonatele x == 0 și y == 0 va apărea pe centrul ecranului. Cu toate acestea, atunci când se afișează obiectul joacă, de asemenea, un rol mare la distanța camerei (z). Pentru două noduri cu aceeași x și y, având o valoare de vârf mai mare de z va apărea mai aproape decât celălalt.

Aceasta se numește o proiecție în perspectivă:

Și din fericire pentru noi, matricea 4x4 poate efectua această proektsiyu¹:

Ne-am mutat din spațiul camerei (toate nodurile sunt definite în raport cu aparatul de fotografiat) în spațiul omogen (toate nodurile sunt într-un cub mic Tot ce se află în interiorul cubului. - este afișat pe ecran).

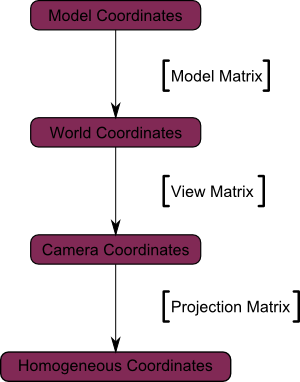
Acum, uita-te la următoarea imagine, astfel încât să puteți înțelege mai bine ceea ce se întâmplă cu proiecția. Înainte de proiecție avem obiecte albastre în spațiul camerei, în timp ce figura roșie prezintă o imagine de ansamblu a camerei, adică. E. Toate ceea ce vede aparatul de fotografiat.

Utilizarea matricei de proiecție au următoarele efecte:

În această imagine, o camera imagine de ansamblu este un cub, iar toate obiectele sunt deformate. Obiectele care sunt mai aproape de camera sa para mai mare, iar cei care sunt mai departe - mici. La fel ca în realitate!

Așa cum ar arata:

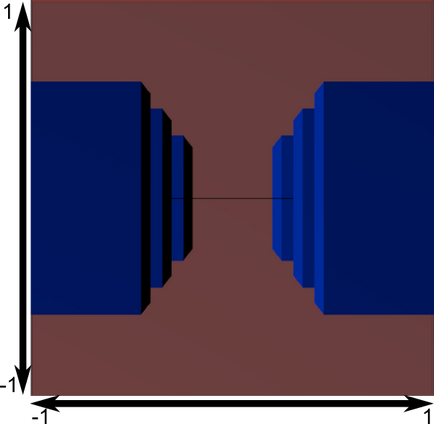
Imaginea este pătrat, astfel încât următoarea transformare matematică aplicată pentru a întinde imaginea în funcție de dimensiunea reală a ferestrei:

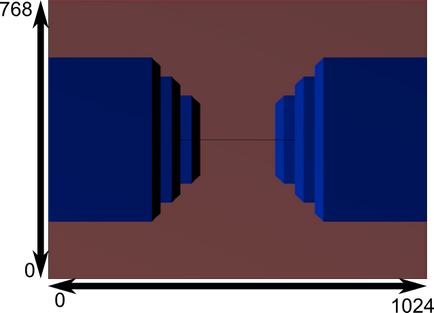
Și această imagine este ceea ce va fi afișată de fapt.

## Merge transformare. matrice ModelViewProjection

... Doar matricea de transformare standard, pe care le iubesc deja!

• Primul pas - crearea matricei noastre MVP. Acest lucru trebuie făcut pentru fiecare model pe care le afișați.

• Al doilea pas - pentru a transmite acest lucru în GLSL:

• Al treilea pas - utilizează datele obținute în GLSL, pentru a transforma noastre topuri.

• Gata! Acum avem un triunghi ca în Lecția 2, încă situat la originea (0, 0, 0), dar acum vom vedea pe termen lung din punct (4, 3, 3).

În Lecția 6, veți învăța cum să modificați aceste valori dinamic folosind tastatura și mouse-ul pentru a crea un aparat de fotografiat pe care l-ați utilizat pentru a vedea în jocuri. Dar, în primul rând, învățăm cum să dea acest model de culoare (Lecția 4) și textura (Lecția 5).

• Încercați să schimbați valorile GLM :: perspectivă
• În loc de a folosi o proiecție în perspectivă, încercați să utilizați ortogonală (GLM: orto)
• Schimbarea ModelMatrix la traducere, rotație și scalarea a triunghiului
• Folosește loc de muncă anterior, dar cu o ordine diferită a operațiunilor. Notă rezultatul.