Exponențială Proprietățile funcției de grafice cu formula
Proprietățile de bază ale graficului funcției exponențiale, zona determinând o multitudine de valori, formula de bază, creșterea intervalelor și scădere. Considerăm derivarea funcției exponențiale și pentru a găsi derivatul său. Precum și, extinderea integrală serie de putere și de reprezentare prin numere complexe.
definiție
Funcția exponențială este o funcție y (x) = a x. în funcție de exponent x. la o valoare de bază fixă a gradului de un.
Domeniul funcției exponențiale, o multitudine de valori
Luați în considerare funcția exponențială
y (x) = a x.
Presupunem că baza puterii este un număr întreg pozitiv:
a> 0.
Apoi, functia y (x) = a x este definit pentru orice x. Domeniul ei:
- ∞
0
y = 1
Graficul funcției exponențiale
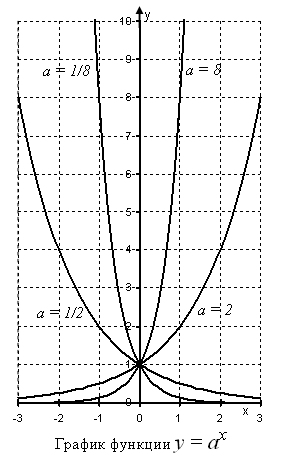
y (x) = a x
pentru patru valori ale nivelului de bază. a = 2. a = 8. a = 1/2 și a = 1/8. Graficul arată că atunci când a> 1 funcția exponențială crește monoton. Grad mai mare de bază a. creșterea puternică. când 0
Proprietățile funcției exponențiale
formula de bază
Când exponent x este un număr natural x = n. expresie a n este produsul de n factori:
Pentru orice valoare a lui x este determinată de o funcție exponențială, astfel încât are toate proprietățile exponent natural.
Formula de transformare la funcția exponențială cu o altă bază de grade:
Când b = e. Obținem o expresie a funcției exponențiale de expozant:
valori particulare
Extremele, creștere, scădere
Funcția exponențială este monoton, deci nu are Extrema. Proprietățile sale principale sunt prezentate în tabelul.
Funcția exponențială inversă cu nivelul de bază este logaritmul în baza a.
Diferențierea funcție exponențială
Pentru diferențierea funcției exponențiale, baza sa trebuie să fie adus la numărul e. se aplică tabelul de derivat și conducă pentru diferențierea unei funcții compozit.
Pentru a face acest lucru, trebuie să utilizați proprietatea logaritmi
iar formula derivată din tabel:
.
Să se dea funcția exponențială:
.
Noi da la baza e.
Din derivații de masă au (înlocuiți variabila x la z):
.
Ca - este constantă, atunci derivata z este egală cu x
.
Conform regulii de diferențiere o funcție compozit:
.
Derivata funcției exponențiale
Un exemplu de diferențierea funcției exponențiale
Găsiți derivatul
Mai 3 y = x
Ne exprimăm baza funcției exponențiale de numărul e.
3 = e ln 3
atunci
.
introducem o variabilă
.
atunci
Exprimarea prin numere complexe
Luați în considerare funcția unui număr complex z:
f (z) = z
unde z = x + iy; i 2 = - 1.
Ne exprimăm r constant complex prin intermediul modulului și argumentul cp.
a = r e i cp
atunci
.
Argumentul cp nu este definit în mod unic. În termeni generali,
φ = φ 0 + 2 πn.
unde n - număr întreg. Prin urmare, funcția f (z) de asemenea nu este clar. Foarte des se ia în considerare de primă importanță
.