Dreptunghi - un paralelogram cu diagonalele egale
Unul dintre semnele dreptunghiului este egalitatea diagonalelor. Aceasta este, în cazul în care diagonala unui paralelogram sunt egale, atunci este un dreptunghi.
Pentru a demonstra acest dreptunghi caracteristică, paralelogram privire la ABCD, a cărui diagonalele AC și BD sunt egale. Trebuie să dovedim că, în acest caz, ABCD - un dreptunghi. Pentru a dovedi acest lucru, este suficient să se demonstreze că unul dintre colțurile paralelogramului directe, adică. A. Pentru o alta caracteristica a dreptunghiului este un paralelogram, care are cel puțin un unghi drept.
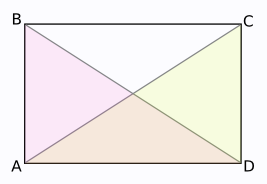
Luați în considerare paralelogramului în triunghiuri ABD și ACD. Ei BD și AC părți sunt egale, adică. Pentru a. Este diagonala, care sunt egale. AB și CD sunt egale ca paralelogram opus. O comună AD parte. Astfel, ΔABD = ΔACD pe trei laturi.
Un colț al triunghiului corespunde unghiului ABD D ACD triunghi. Din egalitatea de mai sus de triunghiuri, rezultă că aceste unghiuri sunt egale între ele: ∠A = ∠D.
Suma unghiurilor paralelogram învecinate sunt întotdeauna egale cu 180 °. Acest lucru rezultă din faptul că colțurile adiacente ale paralelogramului sunt unghiuri de tăiere unilaterală între paralele și drepte. Deci, în acest caz, AB || CD și AD - secant De aceea, ∠A + ∠D = 180 °.
Dacă unghiul A este egal cu unghiul D, și împreună alcătuiesc 180 °, fiecare dintre aceste unghiuri este de 90 °. Astfel, am identificat nu una, ci două unghiuri drepte într-un paralelogram. Din aceasta rezultă că acesta este un dreptunghi. Teorema că, dacă un paralelogram diagonalele sunt egale, atunci este un dreptunghi, dovedit.
Pot fi formulate și teorema conversa: diagonalele dreptunghiului sunt egale. Asta este, nu este dat un dreptunghi, și este necesară pentru a dovedi că diagonalele sale sunt egale.
Și în acest caz, ne putem limita la triunghiuri ABD și ACD. Deoarece prin ipoteză, ne-am dat dreptunghi, unghiul A este egal cu unghiul D, cu condiția. Partidul AD general și AB și CD sunt egale ca laturile opuse ale unui paralelogram (sau dreptunghi). Triunghiurile ABD și ACD sunt egale pe ambele părți sau de colț, între, sau două picioare ale unui triunghi dreptunghic.
Din egalitatea de triunghiuri, rezultă că părțile respective AC și BD sunt egale. Și ei au chiar o diagonală a ABCD dreptunghi. Astfel, se dovedește că, dacă un anumit dreptunghi, atunci diagonalele sale sunt egale între ele.