Cum de a găsi un unghi central de
Dacă cunoscută raza (R) a cercului și lungimea arcului (L), care corespunde unghiului central de necesar (θ), poate fi calculată în grade și în radiani. Circumferința completa definită prin formula 2 * π * R corespunde unghiului central al 360 ° sau două numere Pi, dacă este folosit în loc de grade radiani. Prin urmare, începe de proporțiile 2 * π * R / L = 360 ° / θ = 2 * π / θ. Exprimă din acesta unghiul central în radiani θ = 2 * π / (2 * π * R / L) = L / R sau grade θ = 360 ° / (2 * π * R / L) = 180 * L / (π * R) și se calculează răspunsul prin formula.
Prin lungimea coardei (m), puncte de cerc care definește un unghi central (θ) conectarea, valoarea sa poate fi calculată dacă raza cunoscută (R) al cercului. Pentru a face acest lucru, ia în considerare triunghiul format de cele două raze și o coardă. Acesta este un triunghi isoscel, toate laturile care sunt cunoscute, și au nevoie pentru a găsi un unghi, situată vizavi de bază. Sinus este raportul dintre jumătate din lungimea de bază - coardă - de două ori lungimea unei laturi - raza. Prin urmare, utilizați pentru calcularea funcției sinus inverse - arcsinus: θ = 2 * arcsin (½ * m / R).
Cunoașterea zonei (S) sector de cerc, o rază limitată (R) a unghiului (θ) central și arcul unui cerc, de asemenea, permite să se calculeze valoarea acestui unghi. Pentru a face acest lucru, să dubleze raportul dintre suprafața și raza cvadratura: θ = 2 * S / radicalul R.
Unghiul central poate fi specificat în fracțiuni de rotație completă sau cu unghi drept. De exemplu, pentru a găsi un unghi centrală care corespunde unui sfert de rotație completă, împărțiți la 360 ° timp de patru: θ = 360 ° / 4 = 90 °. Aceeași cantitate în radiani trebuie să fie egală cu 2 * π / 4 ≈ 3,14 / 2 ≈ 1,57. Unghiul extins este pe jumătate plină revoluție, deci, de exemplu, un unghi centrală care corespunde unui sfert din acesta va fi jumătate din valorile calculate mai sus în grade sau radiani.
A lua legatura cu funcție sinus trigonometrică se numește sinusul inversă. Se poate presupune valori situate în jumătate a numărului Pi în pozitiv și în partea negativă, măsurată în radiani. Atunci când se măsoară în grade, aceste valori vor fi, respectiv, în intervalul de la -90 ° la + 90 °.
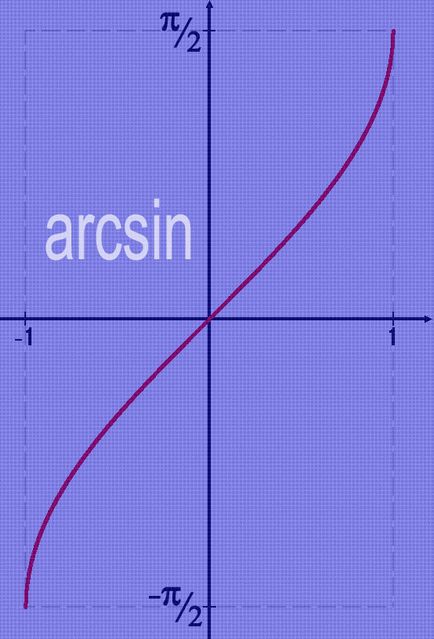
O parte din valoarea „rundă“ a arcsinusul nu este necesar să se calculeze, este mai ușor să-și amintească. De exemplu: - Dacă argumentul funcției este zero, atunci valoarea sinus arc este de asemenea egal cu zero; - arcsinus de 30 ° este egal cu 1/2 sau 1/6 din numărul Pi atunci când este măsurat în radiani - arcsinus de -1/2 este egal cu -30 ° sau 1/6 din radiani număr Pi; - arcsinus 1 este de 90 ° sau 1/2 din numarul radiani Pi; - arcsinus -1 este -90 ° sau 1/2 din numărul Pi radiani;
Pentru a măsura valorile funcției altor argumente simple pentru a utiliza calculator standard Windows, dacă la îndemână este computerul. Pentru a lansa calculator, deschideți meniul principal pe butonul „Start“ (mouse-ul sau apăsarea tastei WIN), du-te la „Toate programele“, secțiunea și apoi, sub „Accesorii“ și apoi faceți clic pe opțiunea „Calculator“.
Comutați interfața de calculator pe modul de operare, care vă permite să calculeze funcțiile trigonometrice. Pentru a face acest lucru, se deschide în secțiunea de meniu „View“ și selectați „Inginerie“ sau „Știința“ (în funcție de sistemul de operare).
Introduceți valoarea argumentului, care este necesar să se calculeze tangenta cu arc. Acest lucru se poate face prin clic pe butonul mouse-ului, interfața calculator, sau prin apăsarea tastelor de pe tastatură sau prin copierea unei valori (CTRL + C), și apoi introducându-l (CTRL + V) în calculator câmp de intrare.
Selectați unitățile în care aveți nevoie pentru a obține rezultatele funcției. Următoarele câmpuri de intrare sunt plasate trei opțiuni din care trebuie să le selectați (făcând clic pe ea cu mouse-ul) - unul grade, radiani, sau excitat.
Se pune o bifă, care inversează funcțiile specificate în butoanele de interfață de calculator. Pe lângă acesta se află la o scurtă inscripție Inv.
Faceți clic pe butonul păcat. Calculator inversează legat de funcția ei se va face calculul și vă prezentăm rezultatul în unitățile menționate.
O sarcină comună este de a calcula suprafața geometrică a unui segment circular - al cercului definit de o coardă și coardă corespunzătoare unui arc de cerc.

Suprafața unui segment circular este egal cu diferența dintre suprafața care corespunde unui sector circular și zona triunghiului format de razele segmentului sector și segmentul coardă delimitând corespunzătoare.
Lungimea coardei, strângând cercului este egală cu valoarea unei. măsură arc Gradul corespunzător coardă este de 60 °. Găsiți zona unui segment de cerc.
Triunghiul format de cele două raze și coardă este isoscel, astfel încât înălțimea trase din vârful unghiului central în partea laterală a triunghiului format de coarda va fi, de asemenea o bisectoare a unghiului centrale, împărțind-o în două și o mediană împărțirea în jumătate din coardă. Știind că sinusul un unghi într-un triunghi dreptunghic egal cu raportul dintre piciorul opus ipotenuzei, se poate calcula raza:
Sin 30 ° = a / 2: R = 1/2;
Zona sectorului care corespunde unui anumit unghi poate fi calculat folosind următoarea formulă:
Sc = πR² / 360 ° * 60 ° = πa² / 6
Zona sectorului triunghiului corespunzător se calculează după cum urmează:
S = 1/2 ▲ * ah, în cazul în care h - înălțimea este desenată din partea de sus a unghiului central al coardei. Prin Teorema lui Pitagora h = √ (radicalul R-a² / 4) = √3 * a / 2.
Zona segment, calculat ca Sseg = Sc - S ▲, egal cu:
Substituind valoare numerică în locul valorii unui, se poate calcula cu ușurință valoarea numerică a segmentului de suprafață.
Raza cercului este egală cu valoarea a. măsură arc Gradul, care corespunde segmentului este egal cu 60 °. Găsiți zona unui segment de cerc.
Zona sectorului care corespunde unui anumit unghi poate fi calculat folosind următoarea formulă:
Sc = πa² / 360 ° * 60 ° = πa² / 6
Zona sectorului triunghiului corespunzător se calculează după cum urmează:
S = 1/2 ▲ * ah, în cazul în care h - înălțimea este desenată din partea de sus a unghiului central al coardei. Prin Teorema lui Pitagora h = √ (a²-a² / 4) = √3 * a / 2.
În cele din urmă, o zonă de segment, calculat ca Sseg = Sc - S ▲, egal cu:
Soluția în ambele cazuri, este aproape identic. Astfel, se poate concluziona că pentru a calcula aria unui segment în cel mai simplu caz este suficient să se cunoască valoarea unghiului corespunzător arc segment și unul dintre cei doi parametri - raza unui cerc sau lungimea corzii, formând un arc al unui segment de cerc care formează.