Cum de a găsi rădăcinile unei ecuații pătratice

ecuația pătratică - este orice ecuație de forma ax 2 + bx + c = 0, în cazul în care un ≠ 0. Găsirea rădăcinilor unei ecuații pătratice - este aceeași ca soluția ecuației, adică, găsirea valorile „x“. Orice ecuație pătratică poate fi rezolvată cu ajutorul formulei x = (-b +/- √ (b 2 - 4ac)) / 2a. În plus, în funcție de o dat ecuația, puteți utiliza unele dintre tehnicile care fac mai ușor pentru a găsi rădăcinile.

pași Editare

Metoda 1 de la 2:
Folosind formula Edit

Înregistrare dat la tine sub forma ecuației ecuației pătratice. Quadratic ecuație - un polinom de ordinul doi cu o variabilă „x“ și un ≠ 0. [1] Cu alte cuvinte, aceasta este o ecuație cu o singură variabilă (de obicei, „x“), cel mai înalt grad este egal cu 2: ax 2 + bx + c = 0

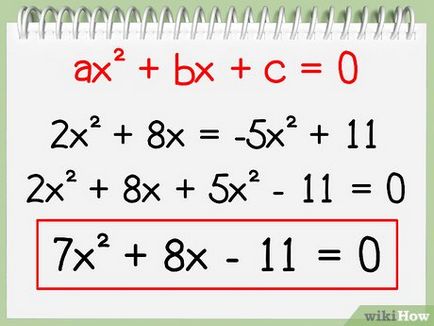
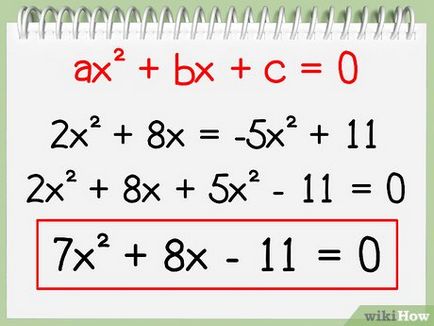
• Pentru a scrie acest lucru pentru a vă în forma ecuația ecuația de gradul doi, își transferă totalitatea membrilor săi de pe partea stângă pentru a rămâne 0. De exemplu, având în vedere ecuația 2x + 2 = 8x -5x 2 pe partea dreapta - 11.
• 2x 2 + 8x = -5x 2 + 11
• 2 2x 2 + 5x + 8x = + 11
• 2 2x 2 + 5x + 8x - 11 = 0
• 7x 2 + 8x - 11 = 0. De notat că această ecuație ia forma ax 2 + bx + c = 0.

Substitut valorile coeficienților a, b, c în formula x = (-b +/- √ (b 2 - 4ac)) / 2a, pentru a găsi valorile "x" (adică, pentru a rezolva ecuația pentru a găsi sau rădăcini). Deoarece ecuația de gradul doi este ax 2 + bx + c = 0, atunci numărul situat în fața x 2. egal cu „a“ la „x“ este egal cu «b», iar termenul este egal cu „c“.

• In exemplul nostru: 7x 2 + 8x - 11 = 0, a = 7, b = 8, c = -11.
• Înlocuind aceste valori în formula, obțineți x = (-8 +/- √ (august 2 - 4 alineatul (7) (- 11))) / 2 (7).

Ia valoarea „x“ (cu semn pozitiv și negativ), urmând operațiile algebrice de bază.

• În exemplul nostru:
• x = (-8 +/- √ (august 2 - 4 alineatul (7) (- 11))) / 2 (7)
• x = (-8 +/- √ (64 - (28) (- 11))) / (14)
• x = (-8 +/- √ (64 - (-308))) / (14)
• x = (-8 +/- √ (372)) / (14)
• x = (-8 +/- 19,29 / (14)

Pentru cele două valori „x“ este necesar să se adauge și scade o valoare. Acest lucru se datorează faptului că rădăcina pătrată a numărului obțineți două valori sunt egale în mărime, dar în semn opus.

• Adăugați și a obține:
• x = (-8 + 19,29) / (14)
• x = 11,29 / 14
• x = 0,81
• Subtract și a obține:
• x = (-8-19.29) / (14)
• x = (-27.29) / (14)
• x = -1,95.
• Astfel, x1 = 0,81 și x2 = -1.95.

Verificați rădăcinile punct deoarece descoperirea rădăcinilor presupune o lungă serie de operații algebrice și, prin urmare, este ușor de a face o greșeală.

• mod rapid și ușor pentru a verifica rădăcinile ecuației - un valorile de substituție ale constantelor a, b, c în calculator on-line ecuații pătratice, de exemplu, aici. [2]

De asemenea, puteți verifica manual răspunsul. Pentru acest substitut găsit valori „x“ în ecuația originală. Dacă egalitatea, rădăcinile credincioșilor (datorită rotunjirii numerelor poate fi menținută aproximativ egale).

• Suplean a găsit valori "x" în ecuația originală 2 7x + 8x - 11 = 0:
• 7 (-1.95) 2 + 8 (-1.95) - 11
• 26.62 - 15.6-11
• 26.62-26.5 = 0,02; 0.02 este aproximativ egal cu 0, adică, egalitatea respectată și X1 - este rădăcina acestei ecuații.
• 7 (0.81) 2 + 8 (0.81) - 11
• 4,59 + 6.48-11 = 0,07; 0.07 este aproximativ egal cu 0, adică, egalitatea respectată și x2 - rădăcina acestei ecuații.

Metoda 2 din 2:
Găsirea rădăcini prin factoring Editare

Factorizarea atunci când a = 1 Editare

Înregistrare dat la tine sub forma ecuației ecuației pătratice. Puteți găsi rădăcinile ecuației, și fără utilizarea formulei, de exemplu, unele ecuații pătratice pot fi rescrise, astfel încât rădăcinile vor fi găsite foarte ușor. Dar, mai întâi, scrieți această ecuație sub forma unei ecuații pătratice: ax 2 + bx + c = 0.

• În această secțiune vom considera numai acele ecuații pătratice, în care a = 1 (ecuația cu un ≠ 1 în secțiunea următoare). De exemplu: x 2 + 7x + 12 = 0.

Ecuația înregistrare în forma (x + _) (x + _) = 0. Descompunerea factorizarea ecuației pătratice - o constatare polinoame în care se obține multiplicarea ecuației inițiale. Deoarece x 2 = x * x, fiecare binom începe cu "x" (x + _) (_ + x) = 0.

• Notă spațiul (marcat de caracterul de subliniere, în continuare, vom explica modul de a găsi numere care sunt inserate în golurile).

Factorizat coeficientul „c“. Adică, trebuie să găsim o pereche de numere, care atunci când este multiplicată ajunge la „cu“.

• În această ecuație, a = 12. Multiplicatorii 12 sunt o pereche de numere 1 și 12, 2 și 6, 3 și 4.

Găsiți o pereche de multiplicatori „C“, care este însumarea dă valoarea „b“ factor (a nu se confunda - uita-te pentru factorii de „b“ nu este necesar).

• În această ecuație, b = 7. multiplicatori "c" sunt o pereche de numere 1 și 12, 2 și 6, 3 și 4. Alegerea unei perechi de numere 3 și 4, din 3 + 4 = 7 (și b = 7).
• În cazul în care nici o astfel de pereche „c“ factori care dă valoarea însumare «b» coeficientul, ecuația descrisă factorize este imposibilă. [3] În acest caz, utilizați o altă metodă de a găsi rădăcinile ecuației pătratice.

Acum, în loc de două goluri în binom (cm. Mai sus) pentru a înlocui un număr de rezultate (adică perechea corespunzătoare de multiplicatori „c“ factor). Așa că așezați ecuația original în factori.

• În exemplul nostru (x + 3) (x + 4) = 0.

Găsiți două valori „x“. Pentru a face acest lucru, fiecare dintre binomi Echivala la 0 și să le rezolve (acest lucru este adevărat, pentru că, chiar dacă una dintre binomi este 0, produsul a două polinoame este 0).

• În exemplul nostru (x + 3) = 0 și (x + 4) = 0.
• x + 3 = 0: x = -3
• x + 4 = 0: x = -4
• Vă rugăm să rețineți că aceste răspunsuri pot fi testate prin aceleași metode ca cele descrise în secțiunea anterioară.

Factorizarea când un ≠ 1 Editare

Așezați coeficientul „a“ la multiplicatorii. Deoarece „un“ stă în fața x 2. atunci fiecare factor va include variabila „x“.

• De exemplu: 2x 2 + 14x + 12 = 0. Aici a = 2 și afișate pe o pereche de multiplicatori 2 și 1. Acesta este primul termen al ecuației 2x 2 = 2 * x.
• Vă rugăm să rețineți că există cazuri când coeficientul „a“ mai multe perechi de multiplicatori. De exemplu, un membru al 8x 2 poate fi compus din următorii factori: 8x * x și 2x * 4x. În acest caz, trebuie să verificați ce pereche de factori pentru extinderea ecuației.

Ecuația înregistrare în formă ((mnozhitel1) + _) ((mnozhitel2) + _). Noi nu începe cu polinoame „x“ ca și în secțiunea anterioară, ca aici, în fața „x“ pot fi unii factori. [4]

• În acest exemplu, o ecuație de scriere (2x + _) (x + _).

Factorizat coeficientul „c“. Adică, trebuie să găsim o pereche de numere, care atunci când este multiplicată ajunge la „cu“.

• În acest exemplu, c = 12; multiplicatori 12 sunt o pereche de numere 1 și 12, 2 și 6, 3 și 4.

În schimb, lacune în produs de polinoame (cm. Mai sus) pentru a înlocui perechea de multiplicatorilor „c“ și de a găsi o pereche care atunci când se multiplice și insumarea membrii binomi da valoare «b». Amintiți-vă că polinoame nu începe aici cu „x“, și cu unii membri ai raportului care conține și o variabilă „x“.

• În acest exemplu, b = 14, iar al doilea termen al ecuației este egală cu 14x. Acest lucru înseamnă că dorim să găsim două numere (o pereche de multiplicatori „c“), dintre care unul este înmulțește cu 2, iar cealaltă la x, și apoi adăugați în sus rezultatele lucrărilor; suma rezultată este egală cu 14x.
• Să considerăm o pereche de multiplicatori 3 și 4: 3 * 2x = 6x; 4 * x = 4x; 4x + 6x = 10x. Nu este potrivit. Numărul Interchange: 4 * 2x = 8x; 3 * x = 3x; 8x + 3x = 11x. Nu este potrivit.
• Luați în considerare o pereche de multiplicatori 6 și 2: 6 * 2x = 12x; 2 * x = 2x; 12x + 2x = 14x. Potrivit! În schimb lacune numere de substituție 6 și 2.

Acum, în loc de două goluri în binom (cm. Mai sus) pentru a înlocui un număr de rezultate (adică perechea corespunzătoare de multiplicatori „c“ factor). Așa că așezați ecuația original în factori. Rețineți că fiecare număr trebuie să fie pus în aplicare (a nu se confunda!) Pentru a obține în cele din urmă raportul corect al «b». După aceea, fiecare dintre binomi Echivala la 0 și de a le rezolva.

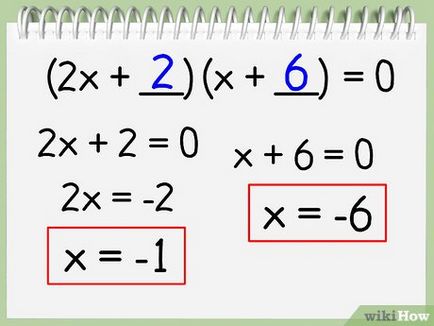
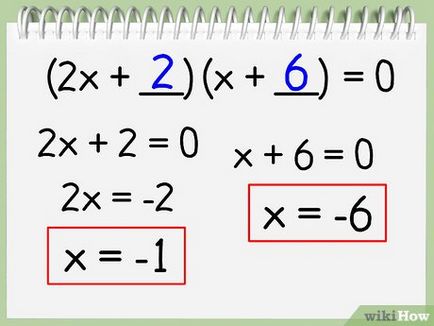
• În acest exemplu: (2x + 2) (x + 6) = 0.
• 2x + 2 = 0
• 2x = -2: x = -1
• x + 6 = 0: x = -6