Componentele elementare și caracteristicile acestora

Link-ul de mai sus a fost identificat ca fiind un model matematic al elementului. În general, link-ul este un model matematic al elementului, care leagă elementele sau orice parte a sistemului. Link-uri, precum și sistemul poate fi descris de ecuații diferențiale ale unui ordin destul de mare și, în general, funcțiile lor de transfer pot fi scrise

Dar ele pot fi întotdeauna reprezentat ca un compus model sau unități elementare, a căror ordine nu este mai mare decât a doua ecuațiile diferențiale.

Desigur, algebra este cunoscut faptul că un polinom de orice ordin poate fi descompus în factori de prim de forma

Prin urmare, funcția de transfer (11), poate fi reprezentat ca un produs de factori principali ai formei (12) și fracții simple ale formei

Link-urile, care transferă funcții sunt date factori principali sau fracții simple. numesc tipuri sau unități elementare.

Termenul proporțional. Proporțional numita unitate, care este descris de ecuația sau, echivalent, funcția de transfer și funcția .Chastotnye temporară a unității de model au forma:

Integrative zveno.Integriruyuschim numita unitate, care este descris de ecuația sau funcția de transfer.

Funcția de transfer de frecvență.

Zveno.Differentsiruyuschim diferențiator numita unitate, care este descris de ecuația sau funcția de transfer. Funcția de transfer în frecvență are forma.

Celelalte funcții de frecvență și de timp au forma:

În primul rând, pentru link-ul aperiodic numita unitate, care este descris de ecuația

sau funcția de transfer.

Această legătură este, de asemenea, numit element de inerțială sau un element inerțială al primului ordin. elementul aperiodice spre deosebire de unitățile discutate mai sus se caracterizează prin doi parametri: T constanta de timp și coeficientul de transmisie k. Funcția de transfer de frecvență

Multiplicarea numărătorul și numitorul cu conjugata complexă a numitor, numărul, obținem

APFC element de întârziere (Fig. 2.7, a) este un semi-cerc, ceea ce nu este greu de verificat ștergerea ecuațiilor parametrice frecvență (2.46) APFC.

LACHH prezentat în Fig. 2.7 b. În practică, de obicei limitată la construcția așa-numitului LACHH asimptotic (linie întreruptă în același Fig. 2.7 b).

Frecvența. în care suprapunerea asimptota, numită frecvență de colț. Exact si asimptotică LACHH difera cel mai puternic cu frecvența de colț; la această abatere de frecvență este aproximativ egală cu 3 dB. Asimptotic LACHH ecuație este:

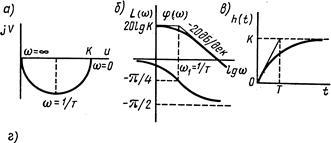
Se obține din ecuația (18). dacă este neglijată sub rădăcină la primul termen, în timp ce - al doilea termen.

Forțându componentă sau link de rapel se numește link prim ordin, care este descrisă de Eq. sau, cu alte cuvinte, funcția de transfer.

Această unitate, cum ar fi aperiodic, caracterizată prin doi parametri: T constanta de timp și coeficientul de transmisie k. Funcția de transfer de frecvență.

Celelalte funcții de frecvență și de timp au forma:

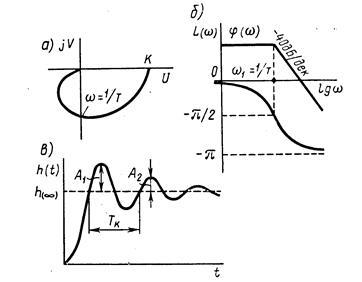
APFC (fig. 2.8, a) este o linie paralelă cu axa imaginară și care intersectează axa reală la punctul U == k. LACHH prezentat în Fig. 2.8 b. Ca și în cazul unei legături aperiodic, în practică, limitată la construcția LACHH asimptotică (linia întreruptă). Frecvența. corespunzătoare punctului de inflexiune al acestei caracteristici este menționată frecvența de împerechere.

Ecuația asimptotică LACHH link booster are forma

Asymptotic LACHH paralel cu axa de frecvență și intersectează ordonata la. și la o înclinare de 20 dB / decadă.

Link-uri de ordinul al doilea vibraționale, conservatoare și aperiodice. Link, care poate fi descrisă de ecuația sau, într-o altă formă

în cazul în care. . sau funcția de transfer

numit oscilatorie dacă. conservatoare în cazul. și link-ul aperiodic de ordinul al doilea, în cazul în care. Coeficientul numit coeficientul de amortizare.

O unitate oscilant. Funcția de transfer de frecvență.

Multiplicarea numărătorul și numitorul cu conjugata complexă a numitorului, obținem funcțiile de frecvență reale și imaginare

Funcția de frecvență de fază variază între 0 și monoton exprimat prin formula

Funcția de frecvență amplitudine

și funcția de amplitudine logaritmică

Ecuația are forma LACHH asimptotice

în care frecvența de împerechere.

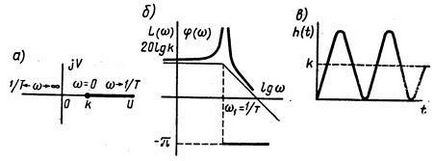
Conform răspunsului tranzitoriu (fig. 2.9, c) puteți defini parametrii nivelului vibrațional după cum urmează.

Coeficientul de transfer k este determinat de valoarea la starea de echilibru a funcției de tranziție. T constanta de timp, iar coeficientul de amortizare poate fi găsit din ecuațiile

în care: - perioada de oscilație, iar amplitudinile de oscilație a două valori stare relativ stabilă adiacente (Figura 2.9 in.).

Funcția de transfer de frecvență.

funcție de frecvență de fază, după cum rezultă din APFC (Fig. 2.10, a)

Este ușor să scrie în jos expresia pentru celelalte funcții de frecvență; LCHH prezentat în Fig. 2.10,6. funcţia de tranziție

Răspunsul pas (Fig. 2.10, c) este un grafic de oscilații armonice.

elementul aperiodice al doilea ordin (). Funcția de transfer (20), cu poate fi transformată

elementul aperiodic de ordinul al doilea poate fi reprezentat ca o conexiune serie de două legături aperiodice de prim ordin. Aceasta nu se referă la numărul de unități elementare.

Unități non-minimal faze. Link-ul se numește minimă fază în cazul în care toate zerourile și polii funcției sale de transfer au negativ sau zero partea reală. Link-ul este numit non-minimal-fază. în cazul în care cel puțin un zero sau pol al funcției sale de transfer are o parte reală pozitivă.

Să ne amintim că zerourile funcției de transfer. în cazul în care - polinoame în s. Chemat rădăcinile ecuației. .. Ie valori astfel, pentru care funcția de transfer merge la zero, și poli - rădăcini. și anume o astfel de valoare s, la care funcția de transfer merge la infinit.

Toate blocurile de construcție discutate mai sus se referă la minim faza. Exemple de unități elementare non-minimal faze sunt unități cu funcții de transfer:

și altele. Pentru nonminimally faze legătură caracteristică că defazaj modul mai mare decât cea a unității de fază minimă având aceeași fază cu frecventa de raspuns non-minimal-link.

Fig. 2.11 arată LCHH unități nonminimally faze cu funcții de transfer (Fig. 2.11, a) și (fig. 2.11, b). LACHH aceste unități coincid cu LACHH aperiodic (fig. 2.7, b) și (booster, b Fig. 2.8) unități. Schimbarea de fază este mai mică decât acesta din urmă: funcțiile de frecvență de fază și componenta forțând aperiodice în valoare absolută nu depășește valoarea. o funcții de frecvență de fază ale unităților respective de non-minimal faze atinge valorile corespunzătoare.

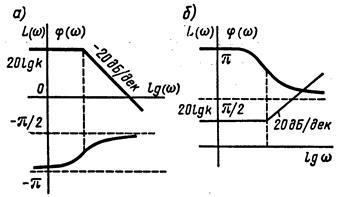
Pentru non-minimal-phase legături includ, de asemenea, o legătură cu funcția de transfer de întârziere pură

Funcția de transfer de frecvență

Pentru restul funcțiilor de frecvență și de timp:

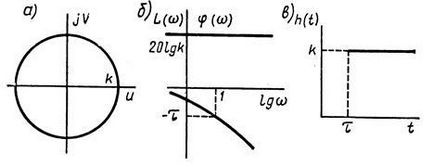
APFC (Figura 2.12, a.) - un cerc centrat la origine și raza k. Fiecare punct al acestei caracteristici corespunde unui număr infinit de frecvențe. LACHH (Fig. 2.12, b) să coincidă cu legătura LACHH freewheeling cu k coeficient de transmisie, LFCHH (Fig. 2.12, b) funcția program -c. Răspuns tranzitoriu este prezentat în Fig. 2.12 în.