Ce este logaritmul

anterior ◈ următoarea

Algebra - o știință complexă și interesant, bazat pe un set de funcții. Luați în considerare ceea ce un logaritm, și care sunt proprietățile sale.

Logaritm - este gradul în care doriți să ridice numărul unei, pentru a obține numărul x.







Algebra știe multe tipuri de logaritmi. Cele mai utilizate pe scară largă

Ce este logaritmul
logaritmilor următoarele tipuri:

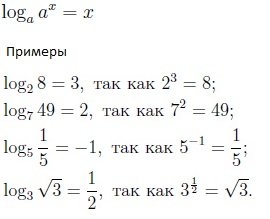
  • baza e naturale = 2,718281, ln notat.
    EXEMPLU: LN1 = 0. LNE = 1;
  • bază zecimală 10, lg notat.
    EXEMPLU: lg100 = 2. log10 2 = 100, la 10 februarie = 100;
  • binar, lb notată (b) sau LB2 b. 2 este o soluție de x = b.
    EXEMPLU: lb16 = 4.

Acestea din urmă sunt utilizate pe scară largă în informatică, teoria informației, și multe secțiuni ale matematicii discrete. Logaritmi ajuta oamenii de stiinta figuranți în identificarea celor mai importante distribuții de probabilitate. Ele sunt, de asemenea, utilizate în genetica.







Cont folosind logaritmi

Matematicienii au cunoscut mult timp proprietățile unice ale logaritmi, precum și posibilitatea de utilizare a acestora, în scopul de a simplifica calcule complexe. Astfel, trecerea la logaritmii:

  • multiplicare poate fi ușor înlocuită prin adăugarea;
  • diviziune - scădere;
  • ridicarea la un anumit grad sau extragerea rădăcinii devine multiplicare sau divizare.

Presupunând folosind logaritmi, să scape de simbol jurnal. În acest caz:

  • Baza și argumentul trebuie să fie pozitiv;
  • Baza trebuie să fie diferită de unitate, deoarece acest număr ridicat la orice putere rămâne neschimbată.

funcţia logaritmică

Funcția logaritmică y = x LOGA (unde a> 0 și ≠ 1) se utilizează în calcule. Printre proprietățile sale sunt următoarele:

  • Domeniul acestei funcții este în setul de numere pozitive;
  • set de valori reprezentate de numere reale;
  • Funcția nu are valorile maxime și minime;
  • Funcția se referă la aspectul general, nu este par sau impar;
  • Funcția nu este periodică;
  • grafic trece prin axele de la punctul (1, 0);
  • la bază, care este mai mare decât una, funcția crește și, dacă mai puțin de o - scade.

Acum aveți o idee de logaritmilor și aplicațiile acestora, precum și proprietățile funcției logaritmică.







anterior ◈ următoarea