Că atât de multe

Un set se numește numărul de diverse obiecte. De exemplu, mulți studenți, mulți studenți, o mulțime de mașini, o mulțime de numere, etc.

În matematică, mulți au considerat mult mai larg. Nu vom îngropa mult în subiect în care se referă la matematici superioare și la început poate face dificil pentru un începător. Vom lua în considerare numai acele care au lucrat.

Setul de numere naturale

Acesta este primul set cu care am început. Numerele naturale numite numerele 1, 2, 3, etc.

Numerele naturale a apărut din nevoile oamenilor să contorizeze alte obiecte. De exemplu, numărul de numărul de pui, vaci, cai, etc. Numerele naturale apar în mod natural atunci când scorul.

În matematică, numerele naturale sunt notate cu litera N. Latină

De exemplu, observăm că numărul 1 face parte din setul de numere naturale. În acest scop, vom scrie numerele 1 în sine, și apoi folosind accesoriile simbolul (∈) indică faptul că unitatea aparține mulțimii N (mulțimea numerelor naturale)

El spune ca: „unul face parte din setul de numere naturale“

Setul de numere întregi

Setul de numere întregi include toate numerele pozitive și negative, precum și numărul 0.

Setul de numere întregi este notat mare Z. majusculă De exemplu, observăm că numărul aparține -5 numere întregi:

Precizăm că 10 aparține mulțimii de numere întregi:

Menționăm că 0 aparține mulțimii de numere întregi:

În viitor, toate numerele pozitive și negative vor fi numite o frază - numere întregi.

Setul de numere raționale

Numerele raționale sunt acele fracțiuni cele mai obișnuite, aflăm astăzi.

număr rațional - un număr care poate fi reprezentat ca o fracție. în cazul în care un - numărătorul, b - numitorul. În rolul numărătorul și numitorul poate fi orice număr, inclusiv numere întregi, pe care le-am discutat mai sus. De exemplu, ne imaginăm că, în locul unui număr necesar de 10, iar în locul b - numărul 2

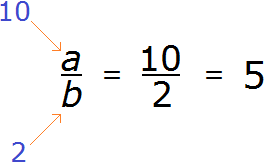
10 împărțit la 2 este 5. Putem observa că numărul 5 poate fi reprezentat ca o fracție, și, prin urmare, este inclusă în setul de numere raționale.

Este ușor de observat că numărul 5 se aplică și la setul de numere întregi. Deci, setul de numere întregi incluse în setul de numere raționale. Deci, în setul de numere raționale includ nu numai fracții ordinare, dar, de asemenea, numere întregi formă -2, -1, 0, 1, 2, etc.

Acum, imaginați-vă că în loc de un număr necesar de 12, și în loc de b - numărul 5.

12 împărțit la 5 este 2.4. Vedem că fracția zecimală de 2.4 poate fi exprimată ca o fracție, și, prin urmare, este inclusă în setul de numere raționale. De aici putem trage concluzia că setul de numere raționale includ nu numai fracții ordinare și numere întregi, dar zecimale.

Am calculat fracțiunea și a primit un răspuns 2.4. Dar am putea evidenția în această fracțiune a întregului:

Atunci când alocă porțiunea întreagă a unei fracții, numărul de spire amestecate. Vedem că numărul mixt poate fi reprezentat ca o fracție. Prin urmare, în setul de numere raționale sunt, de asemenea, forme mixte.

Ca urmare, putem concluziona că setul de numere raționale conțin:

• numere întregi
• fracții
• zecimale
• numere mixte

Setul de numere raționale notate cu litere majuscule Q.

De exemplu, observăm că fracțiunea se află în setul de numere raționale. În acest scop, vom scrie fracțiunea în sine, apoi folosind simbolul accesorii (∈) indică faptul că fracția se află în setul Q (mulțimea numerelor raționale)

Menționăm că fracția zecimală 4.5 face parte din setul de numere raționale:

Subliniem faptul că numărul aparține unui set mixt de numere raționale:

seturi de lecții introductive finalizate. În viitor, considerăm seturi un pic mai profund, și totuși luate în considerare în această lecție va fi de ajuns.

La fel ca lecția?
Alăturați-vă noul nostru grup Vkontakte și începe să primească notificări despre noi lecții