Algoritmi si structuri de date pentru începători de sortare

În această parte, ne uităm la cele cinci algoritmi de bază pentru sortarea datelor în matrice. Să începem cu cel mai simplu - sortare cu bule - și termina „sortare rapidă» (sortarerapidă).
Pentru fiecare algoritm, în plus față de o explicație a muncii sale, subliniem, de asemenea, memoria și complexitatea de timp în cel mai rău, cazul cel mai bun și mediu.
metoda Swap
Pentru a simplifica și de a îmbunătăți lizibilitatea codului vom introduce metoda Swap. care va schimba valorile din matrice de index.
Bubble sortare - este cel mai simplu algoritm de sortare. Acesta trece prin matrice de mai multe ori, în fiecare etapă de mișcare cele mai importante sfârșitul nesortate de matrice.
De exemplu, avem o serie de numere întregi:
Primul pasaj prin matrice, vom compara valorile 3 și 7. Deoarece 7 este mai mare de 3, vom lăsa așa cum sunt ele. Apoi compara 7 și 4. 4 este mai mică de 7, astfel încât să le rearanja trăgând-o poziție de șapte unul mai aproape de sfârșitul matrice. Acum, se pare ca acest lucru:
Acest proces se repetă atâta timp cât șapte nu va veni până aproape la sfârșitul șirului. La final, este comparat cu un element de 8, care este mai mare, și, prin urmare nu există nici o partajare. După ce ne-am dus în jurul matrice o dată, se pare ca acest lucru:
Așa cum sa făcut cel puțin un schimb de valori, trebuie să treacă prin matrice din nou. Ca urmare a acestui pasaj, vom trece la locul de numărul 6.
Și acolo a fost produs din nou cel puțin un schimb, și să treacă astfel, prin matrice din nou.
Următorul pasaj de schimb nu se face, ceea ce înseamnă că oferta noastră este sortată, iar algoritmul a terminat activitatea.
Inserția sortare se execută, care trece prin matrice și se deplasează valoarea dorită la începutul șirului. După procesare poziția următoare, știm că toate elementele înainte de a fi sortate, și după - nr.
Un punct important: sortare inserare tratează elementele matricei în ordine. Deoarece algoritmul ruleaza pe elementele de la stânga la dreapta, știm că tot ce rămâne a indicelui curent - deja sortate. În această figură, este prezentat ca parte matrice sortate crește cu fiecare trecere:
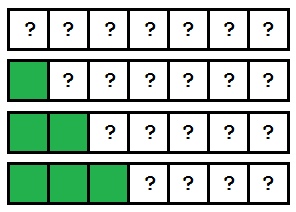
Treptat sortate o parte din matrice crește, iar în cele din urmă, matrice va fi comandat.
Să ne uităm la un exemplu concret. Iată oferta noastră neordonate pe care le vom folosi:
Algoritmul începe cu o valoare a indicelui de la 0 și 3. Deoarece acesta este primul indice al matrice înainte de a fi considerat a fi sortat inclusiv.
În continuare, ne întoarcem la numărul 7. Deoarece 7 este mai mare decât orice valoare în părțile sortate, vom trece la elementul următor.
În această etapă elementele cu indici 0..1 sunt sortate, ci despre elementele cu indici nu 2..N cunoscute.
Ar trebui să verificați valoarea 4. Deoarece este mai mică de șapte, trebuie să-l muta în poziția corectă în partea a sortat matrice. Rămâne întrebarea: cum să-l definească? Acest lucru este realizat prin FindInsertionIndex. Se compară valoarea a trecut la ea (4), cu fiecare valoare în porțiunea sortate până când găsește spațiu pentru a insera.
Așa că am găsit indexul 1 (valori cuprinse între 3 și 7). Metoda Inserare efectuează o inserție, eliminați valoarea inserați matrice, și deplasarea toate valorile de index pentru a insera, dreapta. Acum matrice arată astfel:
Acum, o parte din matrice, pornind de la zero, și se termină cu elementul elementul cu indexul 2, este sortată. Următoarea trecere începe cu indicele 3 și 4. Deoarece valoarea algoritmului, vom continua să facă o astfel de inserție.
Atunci când nu mai este loc pentru inserții, matrice este considerat a fi pe deplin sortate, iar algoritmul este terminat.
Selection Sort - este un hibrid între un balon și sortare inserare. Ca un fel cu bule, algoritmul trece prin matrice de peste si peste din nou, se deplasează o valoare în poziția corectă. Cu toate acestea, spre deosebire de sortare cu bule, se selectează cea mai mică valoare în loc de maxim nesortate. Ca și în cazul sortare de inserție, o parte ordonată a șirului este situat la început, în timp ce în genul balon, ea este la sfârșitul anului.
Să ne uităm la operațiunea de sortare la selecția noastră de matrice nesortate.
În prima trecere prin algoritmul FindIndexOfSmallestFromIndex metoda încearcă să găsească cea mai mică valoare din matrice și mutați-l în partea de sus.
Având o astfel de matrice mică, putem spune imediat că cea mai mică valoare - 3, și este deja în poziția corectă. În această etapă, știm că prima poziție în matrice (indicele 0) este cea mai mică valoare, prin urmare, la începutul șirului este deja sortat. Prin urmare, vom începe a doua trecere - de data aceasta în indicii de la 1 la n - 1.
La a doua trecere, determinăm că cea mai mică valoare - 4. Schimbăm locul lui cu al doilea element, un șapte, apoi 4 se ridică în poziția corectă.
Acum, partea nesortate a matricei începe la indexul 2. Acesta crește cu un element de fiecare dată, prin algoritmul. Dacă pe orice pasaj, nu am făcut nici un schimb, ceea ce înseamnă că matrice este sortat.
După două treceri algoritmul se oprește:
Divide et impera
Pana acum am considerat algoritmi liniare. Ei folosesc o memorie pic in plus, dar are o complexitate pătratică. Pe exemplul algoritmului de sortare îmbinare, ne uităm la tipul de „divide et impera» (divide și cucerește).
Dacă doriți să găsiți o persoană pe nume Petrov, nu va căuta, începând cu litera A și de cotitură pe o singură pagină. Este foarte probabil să descoperi o carte pe undeva. Dacă obțineți litera T, perelistnete câteva pagini înapoi, poate prea mult - la litera A. Apoi merge mai departe. Astfel, flipping înainte și înapoi toate mai puține pagini veți găsi în cele din urmă din dreapta.
Cât de eficiente sunt aceste algoritmi?
îmbinare Sortare
Când mergesort vom împărți în jumătate matrice, atâta timp cât fiecare secțiune nu va fi un element lung. Apoi, aceste zone înapoi în loc (îmbinare), în ordinea corectă.
Să ne uităm la o matrice:
Împărțiți-l în jumătate:
Și vom împărți fiecare parte la jumătate, până când va rămâne o parte a unui element:
Acum, că am împărțit gama în cel mai scurt zonele posibile le îmbina în ordinea corectă.

În primul rând, avem grupuri de două elemente sortat, atunci „colecta“ le în grupuri de câte patru elemente și, în cele din urmă aduna toate împreună într-o matrice de sortat.
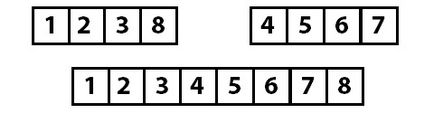
Pentru algoritmul ar trebui să pună în aplicare următoarele operații:
- Operațiunea de divizare recursivă a șirului în grupuri (metoda Sort).
- Fuziunea în ordinea corectă (metoda Merge).
Este demn de remarcat faptul că, spre deosebire de algoritmii de sortare liniare, îmbinare de sortare este de a diviza și matrice lipitură, indiferent dacă acesta a fost sortate inițial sau nu. Prin urmare, în ciuda faptului că, în cel mai rău caz, va lucra mai repede decât liniare, cel mai bun caz, performanțele sale va fi mai mic decât în linie. Prin urmare, un fel de îmbinare - nu cea mai bună soluție atunci când trebuie să sortați matrice parțial uporyadchenny.
public void Sortare (obiecte T [])
în cazul în care (leftIndex gt; = Stânga. Lungime)
articole [targetIndex] = dreapta [rightIndex ++];
else if (rightIndex gt; = Dreapta. Lungime)
articole [targetIndex] = stânga [leftIndex ++];
else if (stânga [leftIndex]. compareTo (dreapta [rightIndex]) lt; 0)
articole [targetIndex] = stânga [leftIndex ++];
articole [targetIndex] = dreapta [rightIndex ++];
sortarerapidă
Rapid sortare - este un alt algoritm, cum ar fi „divide și cucerește“. Acesta acționează prin repetarea recursiv următoarele etape:
- Selectați indicele cheie și împărțiți-l de matrice în două părți. Acest lucru se poate face în diferite moduri, dar în acest articol vom folosi un număr aleatoriu.
- Mutați toate elementele cheie de pe partea dreaptă a matrice, și toate elementele este mai mică decât cheia - spre stânga. Acum, elementul cheie este în poziția corectă - mai mult decât orice element din stânga și din dreapta jos a oricărui element.
- Se repetă primii doi pași până când matrice este complet sortate.
Să ne uităm la algoritmul pe matrice următoarea:
În primul rând, vom selecta în mod aleatoriu un element cheie:
int pivotIndex = _pivotRng. În continuare (stânga dreapta.);
Acum, că știm indicele cheie (4), vom lua valoarea la acel index (6), și se transferă valorile din matrice, astfel încât toate numerele mai mari sau egale cu cheie sunt pe partea dreapta, iar toate numerele este mai mică decât cheia - spre stânga . Vă rugăm să rețineți că, în timpul transferului valoarea indicelui element cheie poate schimba (după cum vom vedea în scurt timp).
Valorile Moving efectuate metoda partiție.
În această etapă, știm că valoarea 6 este pe partea dreapta. Acum vom repeta acest proces pentru partea stângă și dreaptă ale șirului.
Noi numim sortarerapidă metoda recursiv pe fiecare dintre părți. Un element-cheie al partea stângă devine cinci. Când mutați valorile se va schimba indexul său. Principalul lucru - amintiți-vă că este important este cheia, nu indexul său.
Din nou, se aplică sortare rapidă:
Am lăsat una din valoarea nesortate, și pentru că noi știm că totul altceva este sortată, algoritmul se termină.